Силы инерции звеньев в плоском движении

Силы инерции материальных точек звена могут быть приведены к одной точке и, таким образом, представлены их главным вектором и главным моментом. Главный вектор сил инерции, называемый обычно силой инерции звена, равен

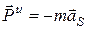, (4.1)

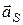где m – масса звена, кг; – ускорение центра S масс звена, м/с². Сила инерциипротивоположна направлению вектора 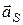и измеряется в ньютонах [н].

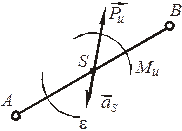
Рассмотрим случай, когда звено совершает плоскопарал­лельное движение и имеет плоскость материальной симметрии, параллельную плоскости его движения. При этом точкой приведения сил инерции звена целесообразно брать его центр масс (рис. 17), так как упрощается выражение момента инер­ционной пары сил – главного момента сил инерции, или инерционного момента. Он оказывается равным

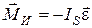, (4.2)

где I_S – момент инерции масс звена относительно оси, проходящей через центр масс перпен­дикулярно плоскости движения, кг·м², 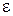– угловое ускорение звена, рад/с².

Инерционный момент М^и имеет размерность [Н·м]. Плоскость, в которой он действует, параллельна плоскости движения звена; он направлен противоположно направлению углового ускорения звена (рис. 17).

Таким образом, в плоском движении инерционная нагрузка звена пред­ставляется одной инерционной силой Р^и, приложенной в точке S и определяемой формулой (4.1), и одним инерционным моментом М^и, определяемым формулой (4.2).

Частные случаи (рис. 18).

Поступательное движение звена (рис. 18, а). Инерционная нагрузка состоит только из одной инерционной силыР^и, определяемой формулой (4.1).

Неравномерное вращательное движение звена (рис. 18, б). Инерционная нагрузка состоит из силы инерцииР^и, определяемой формулой (4.1), и инерционного момента М^и, определяемого формулой (4.2). Модуль полного ускорения центра масс звена в этом случае равен

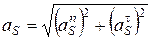, (4.3)

где 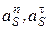– нормальное (центростремительное) и касательное (тангенциальное) ускорения центра масс звена.

Равномерное вращательное движение звена (рис. 18, в). Инерционная нагрузка состоит только из силы инерции Р^и звена, которая в этом случае направлена по линии AS противоположно на­правлению вектора центростре­мительного (нормального) ускорения центра масс звена. Это ускорение равно

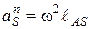(4.4)

и, следовательно, модуль силы инерции будет равен

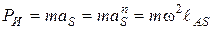. (4.5)

Неравномерное вращатель­ное движение звена при совпа­дении центра масс S звена с его осью вращения А (рис. 18, г). В этом случае инерционная нагрузка звена состоит толькоиз инерционного момента М_И, который находится по формуле (4.2).

Равномерное вращательное движение звена при совпадении центра масс S звена с его центром вращения А (рис. 18, д).

В этом случае а_S=0 и 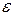=0, следова­тельно,Р_И = 0, М_И = 0.

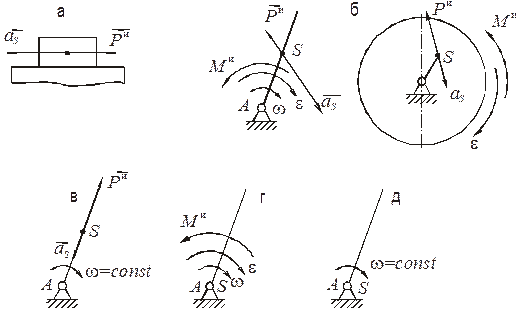Рис. 18. Частные случаи инерционных нагрузок