Произвольные непрерывные распределения
Пример 1. Непрерывная СВ X задана функцией распределения
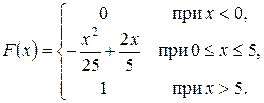
Найти: 1) плотность распределения f(x); 2) M(X); 3) P(1 < X < 2);
4) найти вероятность того, что в трех независимых испытаниях СВ X примет ровно два раза значения из интервала (1, 2).
Решение. 1) Найдем 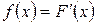 .
.
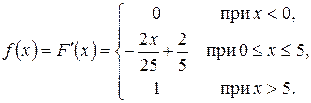
2) Используя формулу (1.17) для нахождения математического ожидания непрерывной СВ X, найдем
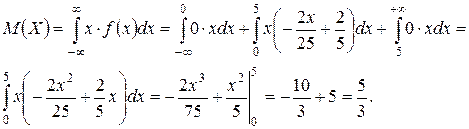
3) Вероятность того, что СВ X примет значения, заключенные в интервале (1, 2), по формуле (1.10) равна
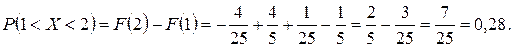
4) Для нахождения искомой вероятности применим формулу Бернулли. Здесь n = 3, m = 2, p = 0,28, q = 1 – p = 0,72.
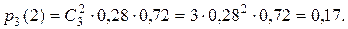
Пример 2. Задана функция f(x)
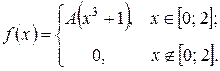
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой СВ X. Найти F(X),
P(1 < X < 3), M(X), D(X).
Решение. Используя свойство нормированности плотности распределения 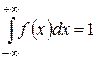 , определим значение параметра A, при котором данная функция задает плотность распределения вероятности некоторой непрерывной СВ X.
, определим значение параметра A, при котором данная функция задает плотность распределения вероятности некоторой непрерывной СВ X.
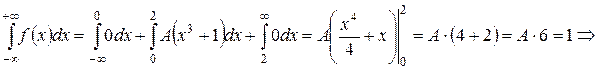
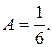
Тогда 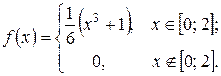
Найдем функцию распределения F(x), используя формулу (1.10) 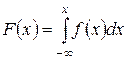
При x Î (– ¥, 0] 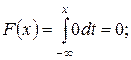
при x Î (0, 2] 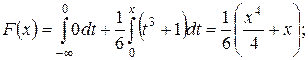
при x > 2 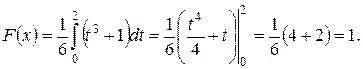
Имеем 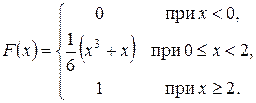
Найдем числовые характеристики:
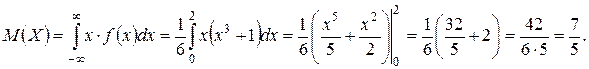
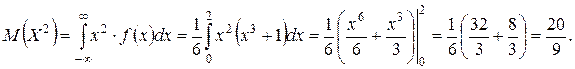
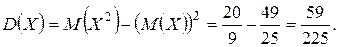
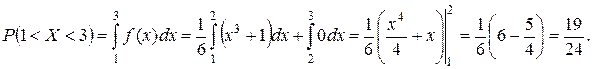
Дата добавления: 2021-12-14; просмотров: 409;











