Асимптотические методы в оценке надежности сложных систем

Оценка надежности сложной системы не только представляет значительные вычислительные трудности, но и требует большого числа данных, сбор которых сопряжен с большими затратами, а иногда просто невозможен. Однако есть широкий класс сложных систем, очень часто встречающихся в практике, для которых работают достаточно точные приближенные оценки. Математические утверждения, в которых изучается предельное поведение объекта в предположении, что какой-то из параметров, описывающих его функционирование, мал (велик), носят название асимптотических. Необходимо изучать надежность сложной системы в предположении малости вероятности отказа за конечный промежуток времени. Более точное описание ситуации следующее.

Пусть X(t)= (x₁(t),...,x_n(t))- процесс, описывающий функционирование изучаемого объекта, как и ранее Q - критическое подмножество в фазовом пространстве. Мы предполагаем, что процессX(t) обладает так называемым свойством регенерации (восстановления). Описательно это означает следующее: существует неубывающая последовательность случайных моментов времени 0 = τ₀< τ₁ < τ₂, ... такая, что в момент τ_п все стохастические свойства процесса X(t)такие же, как и в момент τ₀, а значения процесса до момента τ_п не влияют на его будущие значения. Очень часто случайные моменты τ_п -это моменты попадания X(t)в какое-то состояние.

Например, если мы предполагаем, что капитальный ремонт здания переводит его с точки зрения надежности в некое первоначальное состояние, то моменты окончания ремонтов - это точки регенерации. Следовательно, развитая далее теория применима для ремонтируемых объектов, которые на протяжении их эксплуатации неоднократно восстанавливают свои надежностные характеристики. Можем считать, что траектория процесса X(t)разбивается на циклы (их называют периодами регенерации), после каждого цикла стохастический процесс X(t)как бы начинается заново. Наглядно это можно изобразить, как показано на рис. 4.8.

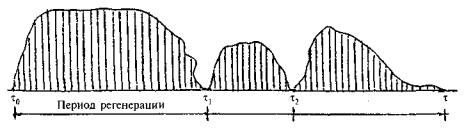
Рис. 4.8. Периоды регенерации объекта в результате ремонтно-восстановительных работ

На каждом периоде регенерации (в нашем случае между ремонтами) возможен отказ системы (например, снижение несущей способности фундамента). Обозначим вероятность этого событияq. Асимптотические результаты для сложной системы верны, когда q мало (математически q ®0). Тогда в достаточно широких предположениях асимптотика вероятности отсутствия отказов в течение времени t имеет вид

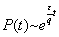(4.10)

где τ - средняя длина периода регенерации (у нас - среднее время между капитальными ремонтами). Заметим, что среднее время эксплуатации системы Т ≈ τ/q,так что в формуле (4.10) можно записать

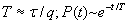(4.11)

Основное достоинство этого результата в том, что требуется ограниченное число параметров. В самом деле, среднее время эксплуатации строительного объекта Т до того, как он придет в полную негодность, для серийных объектов можно оценить. Для уникальных объектов следует пользоваться формулой (4.10). Здесь требуются два параметра: τ и q,причем τ - среднее время между ремонтами - обычно легко оценивается. Трудность - в оценке параметра q. Это достаточно сложная математическая проблема, далеко выходящая за рамки настоящей работы, тем не менее далее предложим один прием для вычисления Т.

Другое достоинство асимптотического подхода в том, что формулы (4.10) и (4.11) дают хорошее приближение для гораздо более широкого класса процессов, чем указано ранее.

В качестве примера 4рассмотрим систему «основание-фундамент» (рис 4.9). Интерпретируя модель «основание-фундамент», будем учитывать три состояния системы: 1 - нормальное состояние для грунта и фундамента; 2 - нарушение свойств грунта и нормальное состояние фундамента; 3 - потеря несущей способности фундамента (критическое состояние).

Мы несколько изменим граф переходов (рис. 4.10).

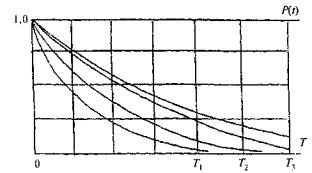
Рис. 4.9. График функции надежности для различных времен Т эксплуатации объекта до его разрушения для примера 4

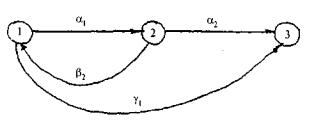
Рис. 4.10. Граф переходов для примера 4
Состояние 3 является критическим множеством

Если β₂ > 0, то это означает, что при нарушении свойств грунта с вероятностью 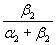происходит его успешное восстановление. Так же, как в примере 1,

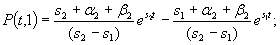(4.12)

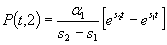(4.13)

только из-за наличия γ₁, корни s₁и s₂вычисляются по следующей зависимости

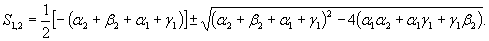
Формулы (4.12) и (4.13) дают точное решение для модели. Мы имеем дело с восстанавливаемой системой, и асимптотическое выражение должно получаться в предположении γ₁ → 0, α₂ →0.

Чтобы упростить выражение, положим γ₁ = 0, а α₂ → 0. Понятно, что предположение γ₁ > 0 вносит не принципиальные, а чисто технические трудности. Итак, при α₂ → 0 имеем асимптотику корней

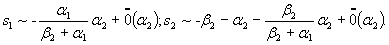
Отсюда 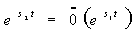и поэтому

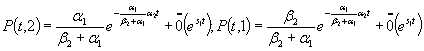
и функция надежности системы может быть описана в следующем виде

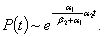(4.14)

Мы получили результат, вытекающий из общих математических теорем. Одновременно можно оценить среднее время эксплуатации системы как

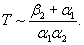
Напомним смысл параметров: 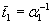- среднее время до возникновения в грунте опасных нарушений физико-механических свойств; (α₂ + β₂)^-1 = θ - среднее время существования грунта в таком состоянии либо до разрушения фундамента, либо до начала восстановительных работ; 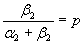- вероятность того, что восстановительные работы начнутся раньше, чем разрушится фундамент, и они будут успешными.

В терминах 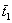, θ, р формула (4.14) примет вид

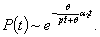(4.16)

В заключение этого параграфа заметим, что основное достоинство асимптотического метода состоит в том, что на процесс не накладывается никаких условий, кроме наличия восстановления (или регенерации), что характерно для большинства строительных объектов.