Нормальное, равномерное и показательное распределения

Пример 1. Математическое ожидание нормально распределенной непрерывной СВ X M(X) = 6, а среднее квадратическое отклонение s(X) = 2.

Найти: 1) вероятность попадания значений СВ X в интервал (2; 9);

2)

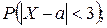
3) интервал, симметричный относительно a, в который попадают значения СВ X с вероятностью g = 0,9642.

Решение. 1) Найдем вероятность попадания значений СВ X в интервал (2; 9).

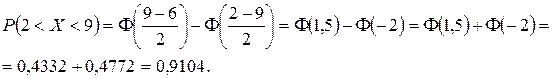
Значения функции Лапласа 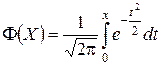взяты из таблицы. Учтено свойство нечетности функции Ф(–X) = – Ф(X).

2) Определим вероятность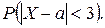

Так как a = M(X) = 6 и s = s(X) = 2, то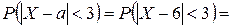

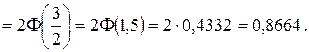
3) Найдем интервал, симметричный относительно a, в который попадают значения СВ X с вероятностью g = 0,9642.

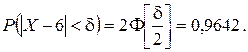Из таблицы значений функции Лапласа находим 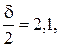то есть d = 4,2. Тогда интервал равен –4,2 < X – 6 < 4,2 и
1,8 < X < 10,2.

Пример 2. Случайная величина Т (час.) – время безотказной работы прибора имеет показательное распределение. Найти вероятность того, что прибор проработает без ремонта не менее 600 часов, если среднее время безотказной работы приборов этого типа равно 400 часам.

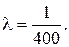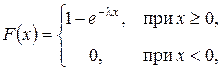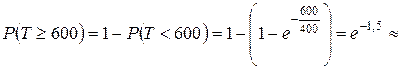Решение. M(T) = 400 час., следовательно, по формуле (1.46) Так как для показательного распределения то 0,2233.

Пример 3. Случайная величина X распределена равномерно на отрезке [a, b]. Найти вероятность попадания случайной величины X на отрезок
[a, b], целиком содержащийся внутри отрезка [a, b].

Решение. Воспользуемся формулой 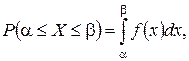где плотность вероятности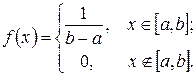

Тогда

.

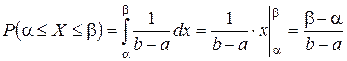Таким образом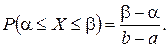

Пример 4. Электропоезда идут строго по расписанию с интервалом
20 мин. Найти вероятность того, что пассажир, подошедший к платформе, будет ожидать очередной электропоезд более 10 мин., а также среднее время ожидания.

Решение. X – время ожидания (мин.) электропоезда, можно считать равномерно распределенной случайной величиной с плотностью:

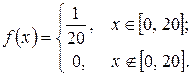
Тогда

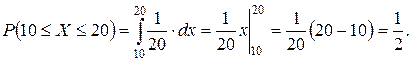
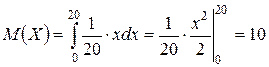и это среднее время ожидания электропоезда.

Пример 5. Автомат изготовливает втулки. Втулка считается годной, если отклонение X ее диаметра от проектного размера по абсолютной величине меньше 1мм. Считая, что случайная величина X распределена нормально со средним квадратическим отклонением s = 0,5 мм и математическим ожиданием a = 0, найти сколько будет годных втулок среди 100 изготовленных, а так же вероятность того, что отклонение от проектного размера будет не менее 0,4 мм и не более 0,8 мм.

Решение. Воспользуемся формулой ( ) 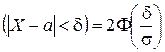при d = 1, s = 0,5 и a = 0.

Получим

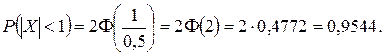
Отсюда следует, что примерно 95 втулок из 100 окажутся годными.

Для нахождения вероятности того, что отклонение от проектного размера будет не менее 0,4 мм и не более 0,8 мм воспользуемся формулой (1.54)

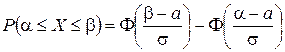при a = 0, s = 0,5, a = 0,4, b = 0,8.

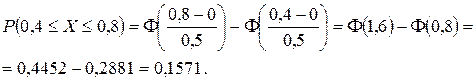
Значения функции Ф(x) находим по таблице.