Случайная величина. Примеры случайных величин

Одним из важнейших понятий теории вероятностей является понятие случайной величины. Под случайной величиной (СВ) понимается величина, которая в результате опыта принимает то или иное значение, причем заранее неизвестно, какое именно. Примерами СВ могут служить: число выстрелов до первого попадания в цель; время безотказной работы прибора; текущий курс рубля по отношению к другой валюте; количество бракованных деталей в партии; температура воздуха в определенной местности в определенное время; суммарная величина выплат страховой компании в течение определенного периода.

Приведем понятие случайной величины в теоретико-множественной трактовке.

Пусть (W, 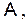P) – произвольное вероятностное пространство. Числовая функция X(w), определенная на пространстве элементарных событий W, называется случайной величиной, если для любого действительного числа x

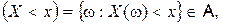(1.1)

где 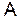– сигма-алгебра событий.

Если в 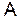включаются все подмножества W, то (1.1) очевидно выполняется.

В дальнейшем случайные величины будем обозначать большими латинскими буквами, а принимаемые ими значения соответствующими малыми.

Для описания СВ следует задать ее возможные значения и определить соответствующие им вероятности.

Законом распределения вероятностей СВ называется любое правило, позволяющее находить вероятности всевозможных событий, связанных со случайной величиной, например, вероятность того, что она примет какое-то значение или попадет в какой-то промежуток.