Способы расчета плеч статической остойчивости при равнообъемных наклонениях

Для того, чтобы вычислить плечи статической остойчивости, координаты ЦВ и поперечного метацентра, необходимо, как это было отмечено в п. 3.1, знать зависимости 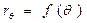для равнообъемных наклонений. По формуле (3.1) 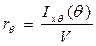, т. е. необходимо знать моменты инерции площадей ватерлиний для равнообъемных наклонений.

В литературе описано большое количество различных способов решения этой задачи, однако наиболее распространены два способа, предложенные А.Н. Кры-ловым и Дарньи. Они основаны на проведении вспомогательных ватерлиний, приближенно отсекающих постоянный объем, с последующим определением расстояния между вспомогательной и соответствующей равнообъемной (дей-ствующей ) ватерлиниями.

Первый способ – способ А.Н. Крылова.

Через точку F пересечения ватерлиний 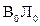и ДПпроводятся все вспо-могательные ватерлинии 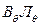через равные углы Δθ (обычно 10º), затем вычис-ляются соответствующие объемы δv_п входящего в воду клина и δv_л выходящего из воды (рис. 3.14). Чаще всего эти объемы не будут равны друг другу, поэтому равнообъемная (действующая) ватерлиния не будет совпадать со вспомо-гательной, а будет проходить под тем же углом на расстоянии ε. Разность между объемами δv_п и δv_л будет приближенно равна объему цилиндра с основанием S ^/ и высотой ε (это возможно, если мы полагаем величину ε малой), т.е. δv_п - δv_л = S ^/ε.

Отсюда

. (3.23)

Здесь S ^/ - площадь вспомогательной ватерлинии, определяемая по известной из главы 1 формулы

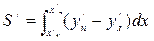, (3.24) где х_н^/ и х_к^/ - абсциссы окончания вспомогательной ватерлинии, снимаемые на ДП.

Ординаты y_п^/ - ординаты правой части вспомогательной ватерлинии, y_л^/ - орди-наты левой части вспомогательной ватерлинии.

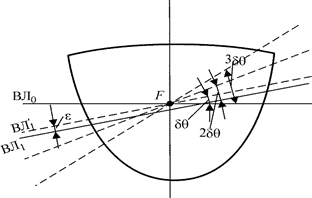
Рис. 3.14. К определению плеч статической остойчивости способом А.Н. Крылова

При малых углах наклонения в выводе теоремы Эйлера мы уже использовали выражения для элементарных объемов клиньев. Для конечного угла крена θ выражения (2.3) можно проинтегрировать, и тогда получим

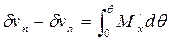, (3.25)

где М_х^/ - статический момент площади вспомогательной ватерлинии отно-сительно оси наклонения. Он равен

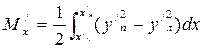. (3.26)

После того, как будет определена ε и проведена действующая ватерлиния, для нее надо снова снимать ординаты y_п и y_л и рассчитывать:

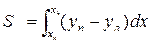- (3.27)

площадь действующей ватерлинии;

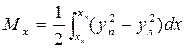- (3.28)

статический момент действующей ватерлинии относительно оси Oy;

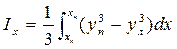- (3.29)

момент инерции площади действующей ватерлинии относительно оси Oy.

Достоинством этого способа является то, что для каждого угла крена элементы ватерлиний вычисляются независимо от вычислений для других углов крена, однако крупным недостатком является необходимость производить такие вычис-ления дважды: сначала для вспомогательной ватерлинии, потом для действую-щей.

Второй способ - способ А.Н. Крылова и Дарньи.

Он заключается в том, что вспомогательные ватерлинии проводятся каждый раз через центр тяжести площади предыдущей действующей ватерлинии. След пер-вой вспомогательной ватерлинии, таким образом, проходит под углом Δθ через точку F₀ пересечения В₀Л₀ и ДП. Затем определяются площадь и статический момент площади вспомогательной ватерлинии, определяется расстояние ε и про-водится первая действующая ватерлиния. Определяется положение центра тяжес-ти ее площади и проводится вторая вспомогательная ватерлиния и т.д. Поскольку каждый раз наклонение увеличивается на малый уголΔθ, удается значительно упростить весь процесс вычислений.

Действительно, формулу (3.25) можно переписать в виде

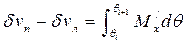, (3.30)

где θ_i и θ_i+1 - предыдущий и последующий углы наклонения.

По правилу трапеций

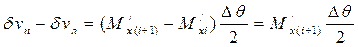. (3.31)

Значение 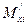(для предыдущей действующей ватерлинии) равно 0, т.к. сле-дующая вспомогательная ватерлиния была проведена через ее центр тяжести. С учетом (3.31) формула (3.25) преобразуется к виду

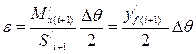. (3.32)

Величина ε при таких построениях очень мала, и можно считать, что площади и другие элементы вспомогательной и действующей ватерлиний одинаковы. Все вычисления производятся только один раз для вспомогательной ватерлинии, ординаты y_п^/ и y_л^/ отсчитываются от ее новой оси поворота.

По предложению Дарньи можно для определения положения центр тяжести действующей ватерлинии не вычислять ε, а ограничиться графическими построениями с использованием . После того, как будет проведена следующая вспомогательная ватерлиния и вычислена ордината , на предыдущей дей-ствующей ватерлинии, необходимо отложить /2 и через полученную точку провести линию, которая по построению и по формуле (3.32) будет находиться на расстоянии ε от вспомогательной, т.е. и будет действующей. Затем на вспомогательной ватерлинии надо отложить от центра тяжести предыдущей действующей ватерлинии величину и перенести ее конечную точку на действующую ватерлинию. Это и будет ЦТ ватерлинии F. Далее весь процесс повторяется (рис. 3.15).

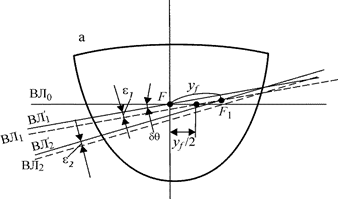
Рис. 3.15. К определению плеч статической остойчивости способом

А.Н. Крылова - Дарньи

В этом способе существенно упрощаются все вычисления, так как при каждом угле наклонения они производятся только один раз для вспомогательной ватерлинии, а для действующей их проводить не надо. Но крупным недостатком является возможность накопления значительных ошибок, поскольку все преды-дущие наклонения могут повлиять на результаты вычислений при последующих наклонениях.

Существуют также способы, в которых равнообъемные ватерлинии при раз­ных углах наклонений не определяются. Рассмотрим предложенный М.Н. Рейновым способ вращения судна около неподвижной оси.

По этому способу судно вра­щается вокруг неподвижной горизонтальной оси рр, па­раллельной ДП. При этом следы ватерлиний на шпангоутах будут прохо-дить через общую точку Р, как показано на рис. 3.16, а. Начальное объемное водоизмещение, соответствующее ватерлинии В₀Л₀ и осадке Т₀ ,равно V₀ .Пусть судно плавает по ватерлинию В₁Л₁с некоторым углом крена 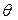. Дадим ма­лое приращение этого угла 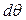, тогда новая ватерлиния В₁Л₁ ^/ будет наклонена к горизонту на угол 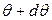(рис. 3.16, б).Изменение водо­измещения при переходе от ватерлинии В₁Л₁к В₁Л₁ ^/ определяется по преобразованной формуле (2.3)

dV=M_x dθ ,(3.33)

где М_х - статический момент площади ватерлинии относительно оси рр. Тогда водоизмещение, соответствующее ватерлинии В₁Л₁ ^/, будет равно

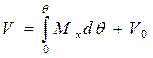.(3.34)

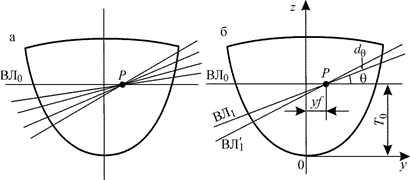
Рис. 3.16. К определению плеч статической остойчивости с помощью способа вращения

Найдем статические моменты водоизмещения относительно координатных плоскостей xOz и хОу. Сначала составим их дифференциалы:

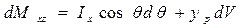;(3.35)

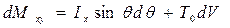. (3.36)

Здесь I_x — момент инерции площади ватерлинии относительно продольной оси, проходящей через точку Р; y_р и T₀ — координаты точки Р. После интегри-рования обеих частей формул (3.35) и (3.36) имеем

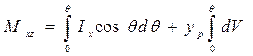; (3.37)

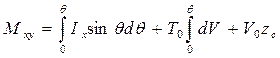. (3.38)

Постоянные интегрирования в этих выражениях представляют собой статические моменты начального водоизмещения. В прямом положе­нии судна координаты ЦВ равны у_с = 0 и z_с ,поэтому постоянные интегрирования равны нулю и соответственно V₀ y_с = 0.

Переменные координаты ЦВ судна, вращающегося вокруг оси рр,опреде-ляются как

= M _xz / V; 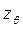= M _xy / V , (3.39)
или с учетом приведенных выше формул

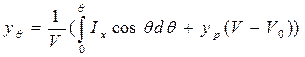; (3.40)

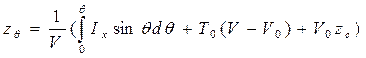. (3.41)

Момент инерции I_х рассчитывается по формуле (3.29). После определения и 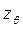легко найти плечо статической остойчивости формы

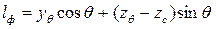. (3.42)

В изложенном способе рассматриваются неравнообъемные наклонения. Так как при изменении угла вращения (крена) водоиз­мещение также изменяется, то построить диаграмму статической остойчивости для одного водоизмещения без дополнительных перестрое­ний невозможно. Поэтому с помощью этого способа определяют зави­симости , а затем с их помощью находят плечо остойчи-вости формы для постоянного водоизмещения. Более подробно это описано в дальнейшем.