Кривые ЦВ и метацентров. Полярная диаграмма

Если для ряда углов крена (10^о, 20^о, 30^о и т.д.) нанести положения ЦВ и метацентров, отложить плечи статической и динамической остойчивости, плечи остойчивости формы и соединить соответствующие точки плавными кривыми, получится диаграмма, изображенная на рис. 3.13.

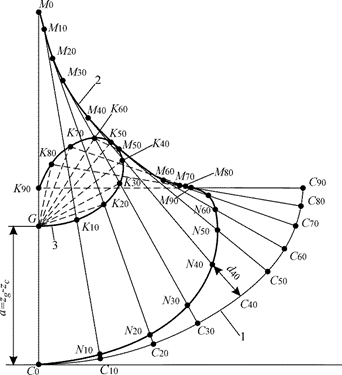
Рис. 3.13. Полярная диаграмма

На этой диаграмме кривая метацентров будет геометрическим местом
центров кривизны кривой ЦВ, т. е. эволютой, или огибающей нормалей; кривая ЦВ будет эвольвентой, или разверткой кривой метацентров. В теории корабля она называется метацентрической оберткой.

Эти кривые обладают следующими свойствами, ясными из самих определений метацентра, ЦВ и т.д.:

1) касательная к метацентрической обертке в любой точке параллельна ватерлинии, отсекающей объем, центром которого является точка касания;

2) линия действия силы поддержания, проведенная из соответствующего ЦВ перпендикулярно плоскости действующей ватерлинии, будет нормальной к метацентрической обертке;

3) радиус кривизны метацентрической обертки в данной точке равен метацентрическому радиусу, вычисленному для площади действующей ватерлинии.

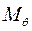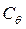Зная положение лишь или для различных углов, можно быстро получить графическим способом плечи статической и динамической остойчивости, плечи остойчивости формы, метацентрические радиусы и т. п.

Если из ЦТ G опустить перпендикуляр на линию действия силы поддержания в точку К, получится плечо статической остойчивости 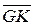. Производя это построение для нескольких углов θ, получим ряд точек 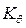и соответствующих плеч статической остойчивости. Огибающая всех точек 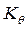называется полярной диаграммой.