Приближенные формулы для определения плеч остойчивости формы.

Существует ряд приближенных формул для расчета плеч остойчивости формы (а следовательно, и плеч статической остойчивости), которые можно использовать в начальной стадии проектирования при отсутствии теоретического чертежа. При этом для определения необходимых в расчетах величин часто применяются статистические данные, полученные при обработке результатов расчетов для близких по форме и размерениям судов, или приближенные формулы для определения элементов плавучести, приведенные в п. 1.16, а также некоторые другие. Они даны ниже.

Плечи остойчивости формы можно аппроксимировать в виде параболических или тригонометрических рядов. Наиболее распространено представление в виде рядов Фурье. Н.А. Заботкин предложил шестичленное разложение

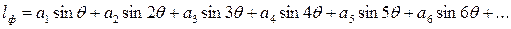(3.45)

В этом разложении свободный член равен нулю и оставлены только синусы, так как плечи остойчивости формы – нечетные функции.

Для коэффициентов выражения (3.45) получены формулы

;

;

;

;

;

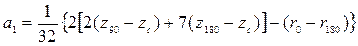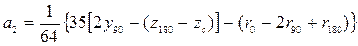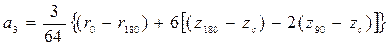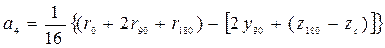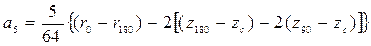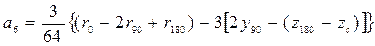. (3.46)

В выражениях (3.46) стоят координаты ЦВ и метацентрические радиусы, рассчитанные соответственно при 0 ^о , 90 ^о и 180 ^о.

Если величины подводного и надводного водонепроницаемых объемов будут равны, т.е. V = V_п / 2 , получится, что r₁₈₀ = r₀ , z₁₈₀ =2z₉₀ - z_c, или иначе z₁₈₀ – z_c= =2(z₉₀ - z_c), и 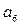= = 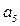0. Таким образом, останется всего четыре члена ряда с коэффициентами

;

;

;

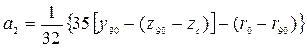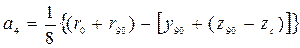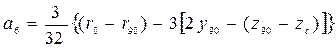. (3.47)

Формула Н.А. Заботкина обращается в четырехчленную формулу В.Г. Власова

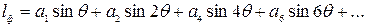(3.48)

Эту формулу можно применять и для других случаев загрузки судов, но она будет тем точнее, чем ближе по величине подводный и надводный водонепрони-цаемые объемы друг к другу, и будет иметь тем большую погрешность, чем величины объемов дальше друг от друга.

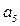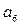От этого недостатка свободна четырехчленная формула, полученная из усло-вия равенства нулю двух последних коэффициентов и . Тогда получится

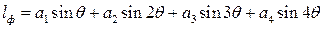, (3.49)

где

;

;

;

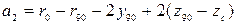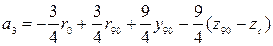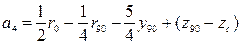. (3.50)

Существуют и четырехчленные формулы, полученные из других соображений, а также трехчленные формулы различных авторов.