Задачи, решаемые с помощью диаграмм статической остойчивости

Предположим, что на судно действует момент М_кр, не зависящий от угла крена. На диаграмме моментов (рис. 3.21) он будет изображаться прямой линией, которая пересекается с кривой восстанавливающего момента M_в в точках А и В. Точки А и В являются точками статического равновесия, так как в них соблю-дается равенство кренящего и восстанавливающего моментов М_кр = М_в.

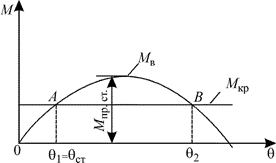
Рис. 3.21. Определение статических углов крена при действии M_кр

В точке А угол θ₁ - угол устойчивого равновесия, так как, если судно вывести из положения равновесия в этой точке, увеличив, например, угол θ₁ на δθ , то, будучи предоставлено самому себе, судно под действием восстанавливающего моментавернется в прежнее положение. Если же вывести судно из положения равновесия, уменьшив угол на δθ, то оно под действием кренящего момента также вернется в прежнее положение. При этом в точке А

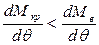. (3.51)

В точке В угол θ₂ характеризует положение неустойчивого равновесия, так как, если вывести судно из положения равновесия, добавив δθ, кренящий момент будет больше восстанавливающего, и оно будет крениться дальше, пока не опро-кинется. Если же θ₂ уменьшить на величину δθ, получится М_кр < М_в , и судноперейдет в положение равновесия θ₁ . В точке В

. (3.52)

Таким образом, только угол θ₁ будет углом статического равновесия. Его обозначают θ_ст .

В случае более сложного закона изменения М_кр(θ) проверка остойчивости в положениях равновесия производится по соотношениям (3.51) и (3.52). Напри-мер, для М_кр,изображенного на рис. 3.22, углы θ₁, θ₃, θ₅ будут углами устойчи-вого равновесия, так как в них выполняется неравенство (3.51), а углы θ₂, θ₄, θ₆ будут углами неустойчивого равновесия, так как в них выполняется неравенство (3.52).

Рис. 3.22. Определение статических углов крена при сложном законе М_кр

Судно может практически безопасно плавать в наклонном положении при углах, меньших θ_max, так как при углах крена, больших θ_max, всегда могут найтись такие внешние силы, которые переведут судно из положения равновесия к углу заката диаграммы, и оно опрокинется.

Момент М_кр= M_max = M_пр.ст называется предельным статическим кренящим моментом. Этот момент судно может выдержать, не опрокидываясь. Угол θ_max будет предельным статическим углом крена.

Разница между М_пр.ст и каким-либо статически приложенным моментом характеризует запас статической остойчивости судна.

В случае действия на судно динамически приложенного кренящего момента условием равновесия будет равенство не моментов, а равенство их работ Т_кр = Т_в , или

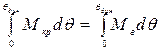, (3.53)

где θ_дин - угол крена, соответствующий углу динамического равновесия (рис. 3.23).

Рис. 3.23. Определение θ_дин

Угол θ_дин может определяться графически из следующих соображений. Инте-гралы являются площадями фигур ODFDEO и OACDEO, ограниченными сверху М_кр и М_в, а справа - абсциссой θ_дин. Уравнивая площади этих фигур, получаем θ_дин. Можно этот угол определить и более просто. Так как дважды заштрихованная площадь OADE0 – общая, можно уравнять площади треугольников ОВА и АCD (рис. 3.24).

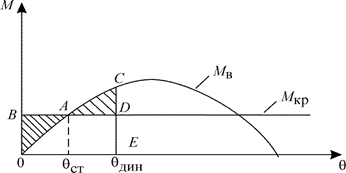
Рис. 3.24. Определение θ_дин по упрощенной модели

Как мы видим, для того же кренящего момента, но приложенного динами-чески, динамический угол крена больше статического, т.е. θ_дин > θ_ст .

Максимальный динамически приложенный кренящий момент, который еще не опрокинет судно, определяется из условия приравнивания площадей ОВА и АCD так, чтобы не осталось незаштрихованных площадей между кренящим и восстанавливающим моментами (рис. 3.25). Этот кренящий момент называется предельным динамическим моментом М_пр.дин . Предельный динамический момент меньше предельного статического момента, т.е. динамически приложенный кре-нящий момент опаснее статически приложенного.

Разница между М_пр.дин и каким-либо динамчески приложенным кренящим моментом характеризует запас динамической остойчивости.

Рис. 3.25. Определение предельного динамического момента

Если кренящий момент зависит от угла крена произвольным образом, все построения, необходимые для определения статических и динамических углов крена и предельных моментов, проводятся аналогично.

При плавании судна в реальных условиях на него практически всегда будут действовать одновременно несколько кренящих моментов различной физической природы (от смещения грузов, от постоянно дующего ветра, от шквала, от дрейфа, от волн, от навала соседнего судна, от рывка буксирного троса, от перекладки руля и т.д.). Это могут быть как статически, так и динамически приложенные моменты. Рассмотрим некоторые наиболее интересные для практики комбинации моментов.

1. Судно плавает с начальным углом крена θ₀ от кренящего момента М₀ , обусловленного перемещением груза (такой момент будет статически приложенным; будем его считать постоянным). Подействовал динами-чески приложенный момент М₁, например, шквал. Необходимо определить статический и динамический углы крена, а также предельные стати-ческий и динамический моменты.

При этом шквал может действовать либо на погруженный навстречу шквалу борт, либо на вышедший из воды борт. На рис. 3.27 (а и б) решается задача определения статических и динамических углов крена для обоих случаев. Считаем, что моменты не зависят от угла крена. Все построения, выполняемые при определении углов, можно повторить и в этих случаях, но только они должны проводиться от угла крена θ₀. Момент М₁ откладывается от момента М_0. Величины же θ_ст и θ_дин измеряются от начала координат.

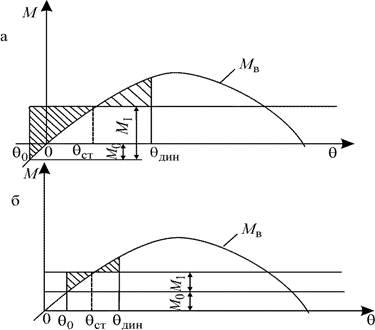
Рис. 3.27. Определение статического и динамического углов крена при одновременном действии момента от груза и шквала

На рис. 3.28 (а и б) решается задача определения предельных моментов. Как мы видим, предельные статический и динамический моменты в случае действия шквала на подветренный борт (рис. 3.28, а) значительнобольше, чем в случае действия на противоположный борт (рис. 3.28, б).

Задача решается совершенно аналогично, если динамически приложенный мо-мент будет иметь другую физическую природу (от рывка буксирного троса и т.д.).

2. Судно плавает с начальным углом крена θ₀ от кренящего момента М₀ , обусловленного постоянно дующим ветром. Подействовал динамически приложенный момент М₁. Необходимо определить предельные стати-ческий и динамический моменты.

Если динамически приложенный момент М₁ не является моментом от шквала, задача решается совершенно также, как и предыдущая. Однако, если налетает шквал, решение будет качественно иным.

Из-за того, что оба момента имеют одну физическую природу, а именно, являются результирующими давления воздуха на надводную поверхность судна, момент от шквала не может суммироваться с моментом от постоянно дующего ветра, а может его только заменить. Это равносильно тому, что ветер как бы мгновенно исчезает, причем у судна остается запас потенциальной энергии для перехода его на такой же угол θ₀ противоположного борта. От этого угла и производятся теперь все построения. При действии шквала на наветренный борт (рис. 3.29, а) предельные моменты будут значительно меньше, чем при действии на подветренный (рис. 3.29, б), что вполне логично, так как в первом случае потенциальная энергия, оставшаяся после прекращения ветра, помогает шквалу опрокинуть судно, а во втором случае шквалу нужно эту энергию преодолевать.

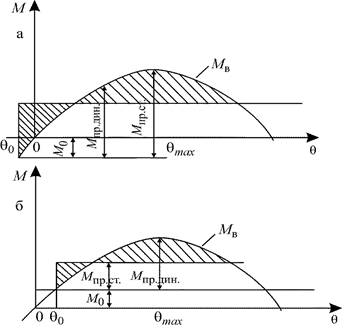
Рис. 3.28. Определение предельных статического и динамического моментов при одновременном действии момента от груза и шквала

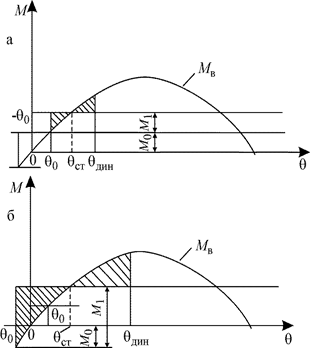
Рис. 3.29. Определение статического и динамического угла крена при одновременном действии момента от ветра и шквала

3. Судно качается на взволнованном море с амплитудой качки θ_r , т.е. испы-тывает воздействие возмущающего момента от волн. Подействовал шквал или динамически приложенный момент другой физической природы. Необходимо определить предельные моменты.

В этой задаче в момент воздействия шквала надо рассматривать также два случая наклонения судна при качке (рис. 3.30): а – судно наклонено навстречу шквалу; б – судно наклонено на другой борт.

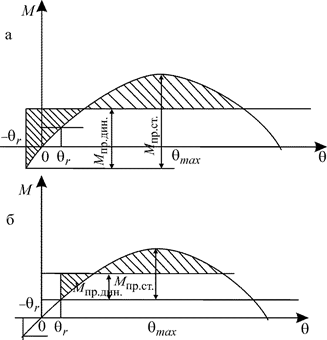
Рис. 3.28. Определение предельных статического и динамического моментов при качке и действии шквала

Как и в предыдущей задаче в первом случае судно обладает энергией от качки для перехода на другой борт, которая суммируется с энергией шквала и помогает ему опрокинуть судно, а во втором случае шквалу надо энергию от качки пре-одолевать. Поэтому в первом случае предельные моменты гораздо меньше, чем во втором. Отсчет их ведется от горизонтальной линии, проходящей через точку пе-ресечения кривой М_в и ординаты, соответствующей амплитуде θ_m противопо-ложного борта.

Задача решается совершенно аналогично, если динамически приложенный мо-мент будет иметь другую физическую природу.