Производная от плеча статической остойчивости по углу крена. Обобщенная метацентрическая высота

Продифференцировав выражение (3.4) по θ, получим

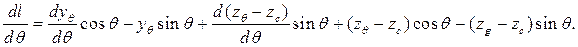(3.12)

В соответствии с (3.2)

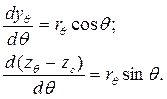(3.13)

Подставив (3.13) в (3.12), получим

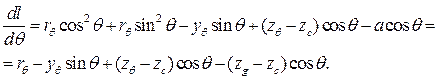(3.14)

При θ = 0 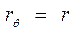; sin θ = 0 ; cos θ =1 ; 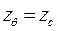и

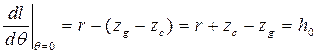, (3.15)

т.е. производная при. θ = 0 равна начальной метацентрической высоте.

По аналогии обозначаем

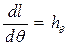, (3.16)

причем 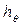называется обобщенной метацентрической высотой. Для нее справедливо равенство 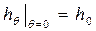, т.е. при θ = 0 она обращается в начальную метацентрическую высоту. При малых углах крена начальная метацентрическая высота характеризует превышение метацентра над ЦТ, т.е. расстояние 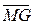. При больших углах крена обобщенная метацентрическая высота также будет характеризовать превышение метацентра над ЦТ. Это будет расстояние 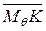(см. рис. 3.3).

На диаграмме статической остойчивости величину 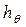можно получить, проведя касательную в любой точке и отложив по горизонтальному направлению угол θ =1 рад (рис. 3.4). Действительно,

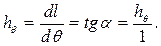
Проведя касательную к диаграмме статической остойчивости в начале координат, т.е. при θ = 0, и отложив по горизонтали I рад, получим начальную метацентрическую высоту 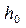. Могут быть случаи, когда начальная метаценри-ческая высота будет близка к нулю (S-образная диаграмма статической остой-чивости на рис. 3.6) или будет отрицательной (диаграмма с отрицательной начальной метацентрической высотой на рис. 3.7).