Расположение на плоскости

Освоение расположения на плоскости требует абстрагирования от привычной ребенку с рождения пространственной среды. Плоскость двумерна, в отличие от трехмерного пространства, а отношение «впереди» в пространстве отличается от отношения «перед чем-то» на плоскости, где оно связано больше с отношением «следовать перед», «предшествовать», т. е. быть расположенным в ряду левее. В связи с этим сначала лучше работать над отношениями «выше», «ниже», т. к. на плоскости эти отношения - аналог пространственного расположения (выше домика - небо, солнце, тучи; ниже - трава, цветы, ежик, земля, дерево). Для характеристики других отношений на плоскости лучше сначала использовать слово «рядом», пстепенно включая в активный словарь ребенка характеристики «справа – слева» ( в ряде случаев они запоминаются и осознаются гораздо позже). Работая на плоскости листа, постепенно также вводим в активный словарь ребенка слова: в центре, в углу, в нижнем углу, в верхнем углу.

Развитие познавательных процессов

Познавательные процессы – это основные формы психической деятельности, позволяющие быстро, глубоко и правильно ориентироваться в явлениях окружающей действительности.

1. Мышление – познавательная деятельность человека по выявлению внешне скрытых особенностей объекта, характеризующаяся обобщенностью и опосредованностью; применение, преобразование и обновление запаса полученных в учении знаний. Мышление теоретическое – познание и обнаружение законов, принципов. Мышление практическое – познание, осуществляемое в ходе практической деятельности, выработка планов и программ действий. Мышление творческое – создание в ходе познания продкта, субъективно или объективно нового. Успешность этого специфического познавательного процесса обеспечивается сформированностью у человека характерных приемов умственных действий:анализ, синтез, сравнение, обобщение и др. Дадим их краткую характеристику:

Сериация - построение упорядоченных возрастающих или убывающих рядов. Классический пример сериации: матрешки, пирамидки, вкладные мисочки и т. д.

Сериации можно организовать по размеру: по длине, по высоте, по ширине - если предметы одного типа (куклы, палочки, ленты, камешки и т. д.) и просто «по величине» (с указанием того, что считать «величиной»), если предметы разного типа (рассадить игрушки по росту). Сериации могут быть организованы по цвету: по степени интенсивности окраски.

Анализ – выделение свойств объекта, или выделение объекта из группы, или выделение группы объектов по определенному признаку.

Например, задан признак: все кислые. Сначала у каждого объекта множества проверяется наличие или отсутствие этого признака, а затем они выделяются и объединяются в группу по признаку «кислые».

Синтез – соединение различных элементов (признаков, свойств) в единое целое. В психологии анализ и синтез рассматриваются как взаимодополняющие друг друга процессы (анализ осуществляется через синтез, а синтез – через анализ).

Н.Б. Истомина отмечает, что «способность к аналитико-синтетической деятельности находит свое выражение не только в умении выделять элементы того или другого объекта, его различные признаки или соединять элементы в единое целое, но и в умении включать их в новые связи, увидеть их новые функции.[19] Задания на формирование умения выделить элементы того или иного объекта (признаки), а также на соединение их в единое целое можно предлагать с первых же шагов математического развития ребенка.

Например:

А. Задание на выбор предмета из группы по любому признаку (2-4 года):

Возьми красный мячик.

Возьми красный, но не мячик.

Возьми мячик, но не красный.

Б. Задание на выбор нескольких предметов по указанному признаку(2-4 года):

Выбери все мячики.

Выбери круглые, но не мячики.

В. Задание на выбор одного или нескольких предметов по нескольким указанным признакам (2-4 года):

Выбери маленький синий мячик.

Выбери большой красный мячик.

Задание последнего вида предполагает соединение двух признаков предмета в единое целое.

Для развития продуктивной аналитико-синтетической мыслительной деятельности у ребенка в методике рекомендуют задания, в которых ребенку необходимо рассматривать один и тот же объект с различных точек зрения. Способом организации такого всестороннего (или, по крайней мере, многоаспектного) рассмотрения является прием постановки различных заданий к одному и тому же математическому объекту.

Например:

Упражнение 1.

Материал: На фланелеграфе набор фигур.

Задание: Одна из фигур в этом наборе лишняя:

с

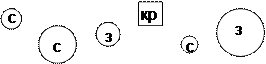
(Квадрат.) Почему? (Все остальные – круги.)

Упражнение 2.

Материал: тот же. Педагог убирает квадрат.

Задание: Оставшиеся круги разделите на две группы. Объясните, почему так разделили. (По цвету, по размеру.)

Упражнение 3.

Материал: тот же и карточки с цифрами 2 и 3 .

Задание: Что на кругах означает число 2? (Два больших круга, два зеленых круга.) Число 3? (Три синих круга, три маленьких круга.)

Упражнение 4.

Материал: тот же и дидактический набор.

Задание: Кто помнит, какого цвета был квадрат, который мы убрали? (Красного.) Откройте коробочки «Дидактический набор». У кого квадраты красные? Какого цвета еще есть квадраты?

- Возьмите столько квадратов, сколько фигур на фланелеграфе. Сколько квадратов? (5) Можно сложить из них один большой квадрат? Добавьте столько квадратов, сколько нужно. Сколько вы добавили квадратов? (4) Сколько их теперь? (9)

***

Традиционной формой на развитие визуального анализа являются задания на выбор «лишней» фигуры (предмета).

Например:

Материал: На доске нарисованы мелом фигурки.

Задание: Одна из них отличается от всех других. Какая?

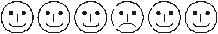
- Чем она отличается?

Задание: Среди этих фигурок найдите лишнюю, отличающуюся от всех других:

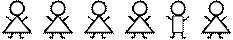
- Почему она лишняя?

Более сложной формой такого задания является задание на выделение фигуры из композиции, образованной наложением одних форм на другие.

Например:

Материал: рисунок на доске

Задание: На этом рисунке спрятано три треугольника. Найдите и покажите их.

Педагог помогает детям правильно показать треугольники (обвести маленькой указкой).

В качестве подготовительных заданий полезно использовать задания, требующие от ребенка синтеза таких композиций на вещественном уровне.

Например:

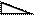Материал: Детям даны по 4 одинаковых треугольника:

Задание: Возьмите два треугольника и сложите из них один. Теперь возьмите два других треугольника и сложите из них еще один треугольник, но другой формы.

- Чем они отличаются? (Один высокий, другой – низкий; один узкий, другой – широкий.)

- Можно ли сложить из этих двух треугольников прямоугольник? (Да.) Квадрат? (Нет.)

***

Психологически способность к синтезу формируется у ребенка раньше, чем способность к анализу. На этой основе можно построить формирование аналитико-синтетического процесса: если ребенок знает, как это было собрано (сложено, сконструировано), ему легче анализировать и выделять составные части.

Сравнение – логический прием умственных действий, требующий выявления сходства и различия между признаками объекта (предмета, явления, группы предметов).

Выполнение сравнениятребует умения выделять одни признаки объекта(ов) и абстрагироваться от других. Для выделения различных признаков объекта можно использовать игру «Найди это»:

- Что (из этих предметов) большое желтое? (Мяч и медведь.)

- Что большое желтое круглое? (Мяч) и т. д.

Ребенок должен использовать роль ведущего так же часто, как и отвечающего, это подготовит его к следующему этапу - умению отвечать на вопрос:

- Что ты можешь рассказать о нем? (Арбуз большой, круглый, зеленый. Солнце круглое, желтое, горячее.)

Вариант: Кто больше расскажет об этом? (Лента длинная, синяя, блестящая, шелковая).

Вариант: «Что это: белое, холодное, рассыпчатое?» и т. д.

Методически рекомендуется сначала учить ребенка сравнивать два объекта, затем группы объектов. Маленькому ребенку легче сначала найти признаки различия объектов, затем – признаки их сходства.

Например:

А. Задания на разделение группы объектов по какому-то признаку (большие и меленькие, красные и синие и т.п.) требуют сравнения.

Б. Все игры вида «Найди такой же» направлены на формирование умения сравнивать. При этом количество и характер признаков сходства может широко варьироваться.

Приведем пример задания, в котором от ребенка требуется сравнение одних и тех же предметов по различным признакам:

Упражнение 1.

Материал: На фланелеграфе изображения двух яблок: маленькое желтое и большое красное. У детей набор фигур: треугольник синий, квадрат красный, круг маленький зеленый, круг большой желтый, треугольник красный, квадрат желтый.

Задание: Найдите среди своих фигур похожую на яблоко.

Педагог по очереди предлагает рассмотреть каждое яблоко. Дети подбирают похожую, выбирая основание для сравнения: цвет, форма.

- Какую фигурку можно назвать похожей на оба яблока? (Это круги. Они похожи на яблоки формой.)

Упражнение 2.

Материал: тот же и набор карточек с цифрами от 1 до 9.

Задание: Отложите направо все желтые фигуры. Какое число подходит к этой группе? Почему 2? (Две фигуры.) Какую другую группу можно подобрать к этому числу? (Треугольник синий и красный – их два; две красные фигуры; два круга; два квадрата – разбираем все варианты.)

Дети составляют группы, зарисовывают и закрашивают их и подписывают под каждой группой цифру 2.

- Возьмите все синие фигуры. Сколько их? (1) Сколько здесь всего цветов? (4) Фигур? (8)

***

Умение выделять признаки объекта и, ориентируясь на них, сравнивать предметы является универсальным, применимым к любому классу объектов. Однажды сформированное и хорошо развитое, это умение затем будет переноситься ребенком на любые ситуации, требующие его применения.

Показателем сформированности приема сравнения будет умение ребенка самостоятельно применять его в деятельности без специальных указаний педагога на признаки, по которым нужно сравнивать объекты.

Классификация - разделение множества на группы по какому-либо признаку, который называют «основание классификации». Классификацию можно проводить либо по заданному основанию, либо с заданием поиска самого основания (этот вариант чаще используется со старшими детьми, т. к. требует определенного уровня сформированности операций анализа, сравнения и обобщения). Следует учитывать, что при классификационном разделении множества полученные подмножества не должны попарно пересекаться и объединение всех подмножеств должно составлять данное множество. Иными словами, каждый объект должен входить только в одно множество и при правильно определенном основании для классификации ни один предмет не останется вне определенных данным основанием групп.

Классификацию с детьми младшего возраста можно проводить:

- по названию (чашки и тарелки, ракушки и камешки, кегли и мячики и т. д.);

- по размеру (в одну группу большие мячи, в другую - маленькие мячики, в одну коробку длинные карандаши, в другую - короткие и т. д.);

- по цвету (в эту коробку красные пуговицы, в эту - зеленые);

- по форме (в эту коробку квадраты, а в эту - кружки; в эту коробку - кубики, в эту - кирпичики и т. д.);

- по другим признакам: что можно и что нельзя есть; кто летает, кто бегает, кто плавает; кто живет в доме и кто в лесу; что бывает летом и что зимой; что растет в огороде и что в лесу и т. д.

Все перечисленные выше примеры – это классификации по заданному основанию: педагог сообщает его детям, а дети выполняют разделение. В другом случае классификация выполняется по основанию, определенному детьми самостоятельно. Во втором случае педагог задает количество групп, на которые следует разделить множество предметов (объектов), а дети самостоятельно ищут соответствующее основание. При этом такое основание может быть определено не единственным образом.

Например:

Упражнение 1.

Материал: На фланелеграфе несколько кругов одинакового размера, но разного цвета (два цвета).

Задание: Разделите круги на две группы. По какому признаку это можно сделать? (По цвету.)

Упражнение 2.

Материал: к предыдущему набору педагог добавляет несколько квадратов тех же цветов (два цвета) и перемешивает фигуры.

Задание: Попробуйте снова разделить фигуры на две группы.

Способ выполнения: Возможны два варианта: по форме и по цвету. Педагог помогает детям уточнить формулировки: дети говорят обычно: «Эти – круги, эти – квадраты».

Педагог обобщает: «Значит, разделили по форме».

В первом упражнении классификация была однозначно задана соответствующим набором фигур только по одному признаку, а во втором – дополнение набора фигур намеренно было произведено таким образом, чтобы стала возможной классификация по двум разным основаниям.

Обобщение – это оформление в словесной (вербальной) форме результатов процесса сравнения.

Обобщение формируется в младшем возрасте как выделение и фиксация общего признака двух или более объектов. Обобщение хорошо понимается ребенком, если является результатом деятельности, произведенной им самостоятельно, например, классификации: эти все - большие, эти все - маленькие; эти все красные, эти всесиние; эти все летают, эти всебегают и т. д.

Все приведенные выше примеры сравнений и классификаций завершались обобщениями. Для младших школьников возможны эмпирические виды обобщения, т.е. обобщения результатов своей деятельности. Для подведения детей к такого рода обобщениям педагог соответствующими образом организует работу над заданием: подбирает объекты деятельности, задает вопросы в специально разработанной последовательности, чтобы «подвести» детей к нужному обобщению. При формулировке обобщения педагог помогает детям правильно его построить, употребить нужные термины и словесные обороты.

Например:

Материал: набор фигур

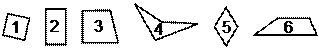
Задание: Одна из этих фигур лишняя. Найдите ее. (Фигура 4.)

Детям незнакомо понятие выпуклости, но они обычно всегда указывают на эту фигуру. Объяснять они могут так: «У нее угол ушел внутрь». Это объяснение для данного этапа вполне подходит.

Вопрос: Чем похожи все остальные фигуры? (У них 4 угла, это четырехугольники.)

* * *

При подборе материала для задания педагог должен следить за тем, чтобы не получился набор, ориентирующий детей на несущественные признаки объектов, что будет подталкивать к неверным обобщениям. Следует помнить, что при эмпирических обобщениях дети опираются на внешние видимые признаки объектов, что не всегда помогает правильно раскрыть их сущность и определить понятие. Например, в приведенном примере фигура 4 в общем тоже является четырехугольником, но невыпуклым. С фигурами такого рода дети познакомятся только в 9 классе средней школы, где в учебнике геометрии формулируется определение понятия «выпуклая плоская фигура». В данном случае первая часть задания была ориентирована на операцию сравнения и выделения фигуры, отличающейся по внешней форме от других. Но обобщение сделано по группе фигур с характерными признаками часто встречающихся четырехугольников. Если у детей возникает интерес к фигуре 4 педагог может отметить, что это тоже четырехугольник, но необычной формы.

Методически формирование у детей способности самостоятельно делать обобщения является крайне важным с общеразвивающей точки зрения. В настоящее время происходят значительные видоизменения как в содержании так и в методике начального обучения математике в школе, целью которых является создание такого математического курса, который активно воздействовал бы на процесс развития у детей как эмпирического, так и в перспективе – теоретического обобщения.

2. Память- включает в себя процессы запоминания, сохранения и воспроизведения. Каждый человек обладает своим, присущим ему, наиболее сильным видом памяти (образной, словесно-логической, эмоциональной и др.). Однако в младшем возрасте два вида памяти больше поддаются целенаправленному развитию: образная и словесная. Развитие словесной памяти проводится путем заучивания различных считалок, стихов. Развитию образной памяти способствуют такие игры:

«Что пропало?» Рассмотрев с ребенком 2-4 небольших предмета на столе (каждый из них ребенок должен уметь называть), педагог накрывает их платком и под платком прячет один в руке. Можно попросить ребенка отвернуться. Постепенно число предметов увеличивается до 5-6. Прятать или убирать можно 2-3 предмета.

«Что изменилось?» На столе выстраивается небольшая сюжетная группа, ребенок должен запомнить ее, затем педагог изменяет 1-2 детали (ребенок отворачивается). Задача ребенка – заметить, что изменилось:

- Мишка сидел на стуле, теперь - на полу. Кукла была в косынке, теперь без нее.

- Машина ехала к домику, теперь едет от домика. Кубик в кузове был синий, теперь – зеленый и т. д.

Для развития долговременного запоминания полезны упражнения с так называемой «отсрочкой», когда педагог просит ребенка воспроизвести материал не сразу, спустя некоторое время, после выполнения каких-то других действий.

3. Внимание- не являясь самостоятельным психическим процессом, внимание тем не менее - важное и необходимое условие эффективности всех видов деятельности человека. Внимание - это направленность и сосредоточенность сознания. Проявляясь как бы внутри познавательных процессов (восприятия, памяти, мышления), внимание способствует повышению их эффективности.

На данном возрастном этапе целесообразно развивать сенсорное внимание (зрительное и слуховое). Формирование и развитие слухового внимания связано с рассказыванием ребенку сказок, стихов, прослушиванием и обсуждением коротких музыкальных фраз (существуют специальные методики развития музыкального слуха и образного музыкального мышления).

Развитие зрительного внимания связано с упражнениями предыдущего пункта: «Что пропало?», «Что изменилось?», «Чем отличаются?» (показываете ребенку два предмета или рисунка предметов, отличающихся одним признаком: кот рыжий и кот серый; кукла большая и кукла маленькая; кукла в платье и кукла в переднике и т. д.).

Развитию запоминания способствуют упражнения типа «Найди такой же» (описаны выше), «Расскажи про него»: педагог показывает ребенку предмет 5-10 сек., затем ребенок по памяти его описывает или находит среди нескольких.

4. Восприятие - отражение в сознании человека предметов или явлений при их непосредственном воздействии на органы чувств. Хорошо развитое восприятие обеспечивает объединение отдельных ощущений в целостные образы вещей и явлений.

Восприятие - это своеобразная деятельность, направленная на обследование воспринимаемого объекта и на создание его адекватной модели (его подобия) в воображении (представлении). В продуктивном восприятии ребенком предмета огромное значение имеет действие, которым пользуется ребенок при восприятии. Развитие перцептивного действия (перцепция – восприятие, схватывание) связывается психологами с развитием сенсорных процессов и рассмтривается как формирование ориентировочной деятельности. Таким образом методически развитие восприятия стимулируется специальным обучением наблюдению (обследованию) и анализу наблюдаемого (обследуемого) предмета, явления и т.п.При этом, сопровождая чувственное восприятие словом, т.е. давая соответствующие названия и определения (пояснения) ребенок собственно осмысливает то, что он наблюдает (обследует). Восприятие – сложный процесс, связанный в том числе и с накоплением определенного запаса образов (эталонов) и сравнением с этими эталонами наблюдаемых (обследуемых) объектов. Не следует думать, что восприятие не поддается развитию и изменению: приобретение личного опыта, усвоение системы общепринятых эталонов, овладение адекватными приемами наблюдения (обследования) изменяет сам способ восприятия, изменяются и его точность, объем, осмысленность.

Например, все упомянутые выше задания на развитие памяти, внимания, мышления будут в то же время «работать» на развитие восприятия.

Поскольку математические объекты являются абстракциями высокого уровня общности, проблема организации их восприятия связана с построением специальных моделей этих объектов, поддающихся сенсорному (зрительному и кинестетическому) восприятию.

Формирование у ребенка запаса адекватных математических «образов восприятия» требует от педагога безупречного владения теоретическими основами элементарной математики и методикой подачи этого материала в доступной ребенку форме, не искажающей при этом смысл понятия.

5. Воображение- процесс преобразования имеющихся представлений, создание новых образов на основе имеющихся. В основе творческого воображения лежит умение строить отражение реальной действительности в новых, неожиданных, непривычных сочетаниях и связях.

Воображение имеет характер аналитико-синтетический и поддается развитию с помощью специальных упражнений (например, система ТРИЗ).

Полезны упражнения вида:

«На что это похоже?»

- на крышу, на шалаш, на стог сена, на букву А немножко и т.д.;

- на руль, на бублик, на колесо;

- на мост, на радугу, на гору и т. п.

«Для чего это можно использовать?»

- для еды; для расчесывания, если нет расчески; для доставания ягод из банки с компотом; для вычерчивания узоров на печенье перед выпечкой; для выкапывания ямки в песочнице и т. д.

«Что из этого получится?»

Используется любая магнитная мозаика, из которой можно собирать «что хочешь», а потом угадывать - что это, кто это. Подойдет любая другая мозаика, позволяющая из 2-4 деталей получить уже что-то осмысливаемое (домик, машина, поезд, человек, птица и т. д.).

«Дорисуй, чтобы что-то получилось»

Вариант: дострой (из палочек, из мозаики), чтобы что-то получилось.

Исследования психологов показывают, что воображение является одним из важнейших факторов, определяющих уровень творческих возможностей человека. С другой стороны, имеются исследования, выявляющие корригируемость развития воображения и развития пространственного мышления человека (поскольку образное мышление является основой пространственного мышления), во всяком случае, для развития математических способностей такая взаимосвязь является очевидной.

Развитие характерных качеств математического мышления