И мгновенного центра ускорений (МЦУ) звена

Для определения МЦС и МЦУ используют теорему подобия, а на плане механизма строят фигуры, подобные фигурам (треугольникам) на планах скоростей и ускорений (рис. 2.3).

Из теоретической механики известно, что плоскопараллельное движение звена механизма в каждый момент времени может быть представлено как вращение вокруг некоторой точки, которую называют мгновенным центром вращения или мгновенным центром скоростей (МЦС). Если данная точка относится к станине (стойке) механизма, т.е. является неподвижной, то соответствующий МЦС называют мгновенным центром скоростей в абсолютном движении рассматриваемого звена. Таким образом, если мы представим, что точка P_V2 принадлежит шатуну (рис. 2.3), то её скорость будет равна нулю.

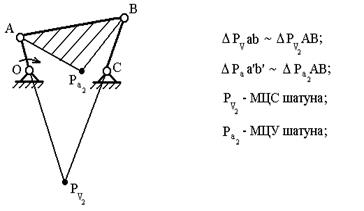
Рис. 2.3. Определение положений мгновенных центров скоростей P_V2 и ускорений Р_а2 шатуна

Если же рассматривается движение звена относительно любого подвижного звена механизма, то соответствующий МЦС называют мгновенным центром скоростей в относительномдвижении рассматриваемых звеньев.

Аналогично может быть найдена условная точка, принадлежащая звену, абсолютное ускорениекоторой в данный момент времени равно нулю. Эта точка называется мгновенным центром ускорений (МЦУ) звена. Если звено механизма совершает сложное плоскопараллельное движение, то меняются и положения МЦС и МЦУ.

Планы скоростей и ускорений кривошипно-ползунного механизма

План скоростей – это чертеж, выполненный в виде отрезков-векторов, показывающих скорость точек в данном положении механизма.

Последовательность построения планов скоростей и ускорений кривошипно-ползунного механизма (рис. 2.4) аналогична той, которая приведена в предыдущем случае. В дальнейшем некоторые подробности (расчёты масштабов, длин m_е, масштабов планов скоростей m_v и ускорений m_а и т.д.) будут пропущены.

План скоростей кривошипно-ползунного механизманачинают строить после построения плана механизма в заданном положении, в выбранном масштабе длин m_L, составления векторного уравнения скоростей и выбора масштаба плана скоростей m_v.

Векторное уравнение скоростей шатуна 2 (рис. 2.4):

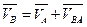
где V_А = w₁ L_OA – скорость точки А, м/с; вектор этой скорости направлен перпендикулярно прямой ОА кривошипа 1 (рис. 2.4) на плане механизма; V_ВА – вектор скорости точки В относительно А; имеет направление, перпендикулярное прямой АВ на плане механизма; V_В – вектор полной (абсолютной), скорости ползуна 3; должен быть параллельным направлению движения ползуна.

Для построения плана скоростей сначала из полюса плана Р_v (рис. 2.4) проводится вектор скорости точки А относительно О – V_А, т.е. векторный отрезок Р_va. Затем через точку апроводится перпендикуляр к прямой АВ плана механизма и через полюс Р_v – прямая, параллельная движению ползуна 3. На пересечении этих двух прямых получается точка b. Направления векторов скоростей V_В иV_ВА обозначают стрелками.

Например, необходимо определить скорость точки S₂, принадлежащей шатуну 2 и расположенной на середине отрезка АВ. Используя теорему подобия, на отрезке ab плана скоростей находят его середину (точка S₂), которая, будучи соединенной с полюсом Р_v, даст вектор V_S2, изображающий абсолютную (полную) скорость точки S₂.

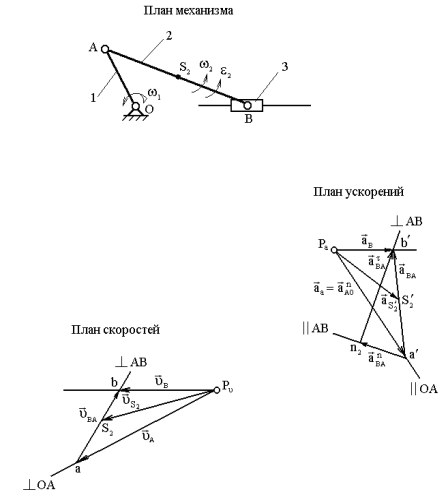Рис. 2.4. Построение планов скоростей

и ускорений кривошипно-ползунного механизма

Рассчитаем величину линейных скоростей и угловую скорость шатуна:

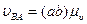, м/с,

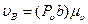, м/с,

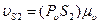, м/с,

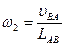, с^-1.

Направление вектора угловой скорости шатуна w₂ определяется следующим образом. Вектор скорости V_ВА условно переносится в точку В плана механизма. Куда он будет вращать шатун относительно точки А, в ту сторону и направлена угловая скорость w₂ шатуна.

План ускорений кривошипно-ползунного механизма строят после того, как будет составлено векторное уравнение ускорений шатуна, учитывая, что он совершает сложное движение:

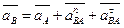
где а_А – ускорение точки А; его величину и направление можно определить, используя векторное уравнение ускорения точки А относительно оси О вращения кривошипа:

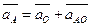
причём ускорение точки А относительно О можно разложить на две составляющие – нормальное ускорение аⁿ_АО и тангенциальное а^t_АО, т.е.:

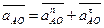
Так как точка О неподвижна и ускорение её равно нулю (а_О= 0 и а^t_АО = 0 при условии, что угловая скорость вращения кривошипа постоянна: w₁ = const и его угловое ускорение e₁ = 0), то векторное уравнение ускорения точки А можно записать в виде:

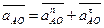
Величина нормальной составляющей ускорения (нормальное ускорение) рассчитывается по формуле:

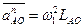
(его вектор направлен по радиусу вращения кривошипа от точки А к точке О).

Затем вычисляется нормальное ускорение точки В относительно А по формуле:

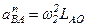
(его вектор направлен от В к А).

После выбора масштаба плана ускорений по формуле:

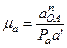
величина нормального ускорения aⁿ_BA переводится этим масштабом в векторный отрезок длиной:

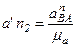, мм.

Затем строится план ускорений (см. рис. 2.4). Из произвольно выбранного полюса Р_а параллельно отрезку ОА плана механизма проводится вектор ускорения aⁿ_AО, длина которого 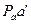была выбрана произвольно при расчёте масштаба m_а. Из конца этого вектора (точки 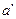) проводится вектор ускорения aⁿ_BA длиной 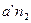, который должен быть параллелен отрезку АВ плана механизма и направлен от точки В к А. Перпендикулярно ему через точку n₂ проводят прямую до пересечения с прямой, проведённой через полюс Р_а параллельно линии движения ползуна 3. Полученная точка их пересечения b' определяет длины векторов ускорений a_BA и a_B.

Для нахождения величины ускорения точки S₂, принадлежащей шатуну, можно применить теорему подобия. При этом необходимо на векторе, изображающем на плане ускорений относительное ускорение a_BA, найти соответствующую точку S₂', делящую отрезок a'b' в той же пропорции, что и точка S₂ делит отрезок АВ на плане механизма.

Угловое ускорение шатуна вычисляется по формуле:

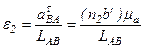, с^-1,

где n₂b' – длина вектора на плане ускорений, изображающего тангенциальное ускорение а .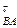

Для определения направления вектора углового ускорения шатуна e₂ необходимо вектор тангенциального ускорения а 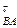условно перенести в точку В плана механизма. Куда он будет вращать шатун относительно точки А, в ту сторону и направлено ускорение e₂ шатуна.

Планы скоростей и ускорений кулисного механизма

Чтобы построить план скоростей, необходимо составить векторное уравнение скоростей. При этом следует иметь в виду, что точка А₁ (рис. 2.5), принадлежащая кривошипу 1, и точка А₂, принадлежащая ползуну 2 и совпадающая на плане механизма с точкой А₁, вращаются вокруг оси О с одинаковыми линейными и угловыми скоростями:

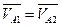иw₁ = w₂.

Если задана величина w₁, то величину линейной скорости рассчитывают по формуле:

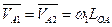, м/с.

Векторы скоростей V_А1 иV_А2 направлены перпендикулярно радиусу ОА₁. Скорость точки А₃, принадлежащей кулисе 3, можно найти по векторному уравнению скоростей:

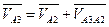
где V_А3А2 – вектор скорости точки А₃ кулисы относительно точки А₂ ползуна, параллельный прямой А₁В плана механизма.

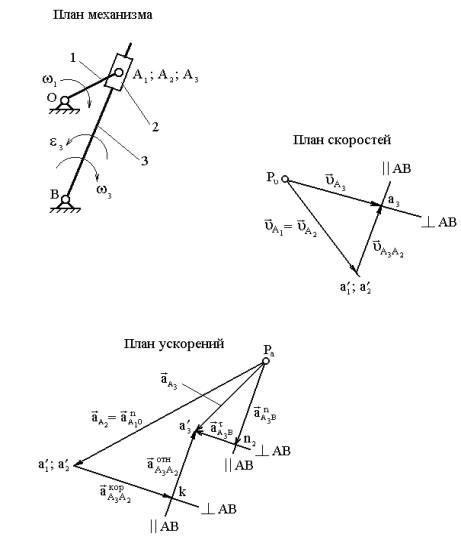
Рис. 2.5. Построение планов скоростей и ускорений

кулисного механизма

После выбора масштаба плана скоростей m_v (см. предыдущие примеры механизмов) строят план скоростей. Из полюса Р_v (см. рис. 2.5) перпендикулярно отрезку ОА плана механизма проводится вектор скорости V_А1, совпадающий с вектором скоростиV_А2 (см. рис. 2.5, вектор 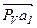). Через точку а₁ проводят прямую, параллельную прямой А₁В, а через полюс Р_v – прямую, перпендикулярную А₁В. На их пересечении получают точку а₃ и наносят направление векторов (стрелки), руководствуясь векторным уравнением скоростей.

Вычисляют величины скоростей:

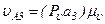, м/с,

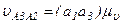, м/с,

где Р_v a₃ и а₁ а₃ – длины векторов, измеренные на плане скоростей.

Угловая скорость коромысла 3 вычисляется по формуле:

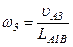,с^-1.

Для построения плана ускорений составляются векторные уравнения:

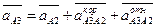
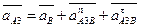
где а_А2 – ускорение ползуна; а 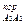– ускорение Кориолиса точки А₃ относительно А₂ (возникает тогда, когда есть относительное движение двух точек с одновременным вращением их вокруг какой-либо оси; в данном случае точка А₃ движется относительно А₂, вместе они вращаются вокруг неподвижной точки В; направление вектора а 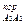определяется так: необходимо условно повернуть вектор скорости V_А3А2 по направлению вращения кулисы 3 – это и будет направление ускорения Кориолиса); а 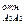– относительное ускорение точки А₃ относительно А₂ (его вектор параллелен А₃В); а_В – ускорение точки В (а_В = 0, так как точка В неподвижна); а 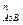– нормальное ускорение точки А₃ относительно В (направление вектора от А₃ к точке В); а 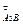– тангенциальное ускорение точки А₃ относительно В (вектор направлен перпендикулярно А₃В).

Вычисление величины ускорения Кориолиса и нормальных ускорений можно произвести по формулам:

а_А2 = а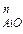 = w 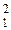L_ОА, м/с²,

а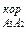= 2w₃ V_А3А2, м/с²,

а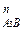= w 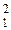L_А3В, м/с².

Масштаб плана ускорений выбирают, используя формулу:

, ,

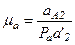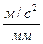где Р_а а'₂ – длина вектора, изображающего ускорение а_А2 на плане ускорений; она выбирается произвольно с таким расчётом, чтобы будущий план ускорений разместился на отведённом месте чертежа и масштаб был удобен для использования в дальнейших расчётах.

Остальные известные величины ускорений переводятся масштабом в векторные отрезки соответствующих длин:

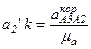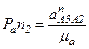, мм; , мм.

Затем строится план ускорений. Из произвольно выбранного полюса – точки Р_а – проводится вектор ускорения а 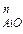с длиной Р_аа'₂. Из точки а'₂ перпендикулярно А₂В проводится вектор ускорения а 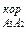с длиной a'₂k. Через точку k проводится прямая, перпендикулярная этому вектору. Таким образом, будет выполнено графическое изображение первого векторного уравнения ускорений из двух, ранее составленных. Затем приступают к построению второго векторного уравнения. Из полюса Р_а параллельно прямой А₃В проводится вектор ускорения а 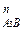длиной Р_а n₂, а через точку n₂ – перпендикулярная ему прямая до пересечения с прямой, проведённой ранее через точку k. На пересечении этих прямых получается точка а'₃. Вектор, соединяющий точки Р_а и а'₃, – полное ускорение а_А3 точки А₃.

Угловое ускорение кулисы вычисляется по формуле

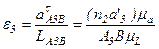, с^-2,

где n₂a'₃ – длина вектора, изображающего на плане ускорений тангенциальное ускорение точки А₃.

Направление углового ускорения определяется, как и в предыдущем примере (для кривошипно-ползунного механизма), по направлению условного вращения кулисы 3 вектором ускорения а 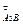: условно перенести этот вектор в точку А₃ плана механизма и посмотреть, в каком направлении он будет «вращать» кулису.