Аналог скорости. Аналог ускорения

Положение любого звена механизма может определяться параметрами: углом j_К относительно какой-либо координатной оси или координатами Х_К и Y_К (рис. 2.6).

Функция положения – это аналитическая зависимость положения или координаты К-го звена (j_К, Х_К или Y_К ) от положения ведущего звена j₁, т.е. j_К (j₁) или X_K(j₁) и Y_K(j₁), где j_К, X_K и Y_K – координаты, определяющие положение К-го звена (ведомого), а угол j₁ – угол, характеризующий положение ведущего звена.

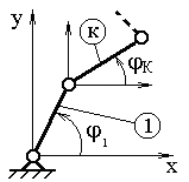
Рис. 2.6. Схема механизма

Аналог скорости. Угловая скорость К-го звена определяется зависимостью:

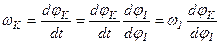, (2.3)

где 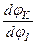– аналог скорости К-го звена (первая передаточная функция) для вращающегося звена, величина безразмерная;

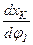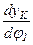и – аналоги скорости К-го звена, движущегося поступательно, величины безразмерные.

Аналог ускорения. Угловая скорость К-го звена определяется зависимостью, получаемой дифференцированием уравнения (2.3) по dt:

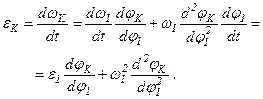
При дифференцировании предполагается, что угловая скорость К-го звена w_к определяется зависимостью:

,

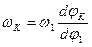а угол j_к является функцией угла j₁:

.

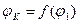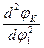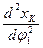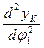Величина – аналог ускорения К-го звена, совершающего вращательное движение, величины и – аналоги ускорения К-го звена, двигающегося поступательно, в проекциях на оси X и Y.

Введение в кинематический анализ понятий аналогов отделяет геометрические свойства механизма от кинематических.

Величину 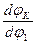называют ещё передаточным отношением, так как выражение 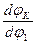можно преобразовать, умножив и разделив его на величину dt:

.

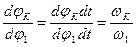Отношение угловых скоростей в механике называют передаточным отношением .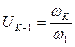

Аналог скорости звена также называют первой передаточной функцией.

Задачи кинематического анализа и пути их аналитического решения приведены в таблице 2.

Таблица 2.1

Задачи кинематического анализа

Функции положения	Задача о скоростях	Задача об ускорениях
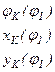
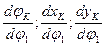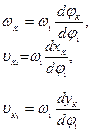
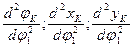Определить функции положения:	Определение аналогов скоростей Вычисление скоростей	Определение аналогов ускорений Вычисление ускорений

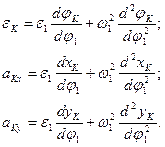
Как следует из приведенной таблицы, для решения задачи о положениях звеньев исследуемого механизма необходимо найти функции положения (j_К или Х_К и Y_К ), предварительно составив векторное уравнение замкнутого векторного контура кинематической цепи и уравнения проекций его на координатные оси Х и Y. Из этих уравнений находят функции положения (зависимости положений исследуемого звена от положения ведущего звена). При известном (заданном) законе движения ведущего звена задаются шагом и вычисляют координаты исследуемых звеньев (угловые координаты для вращающегося звена и прямоугольные для звена, совершающего возвратно-поступательное движение).

Для решения задачи о скоростях необходимо найти аналоги скоростей исследуемых звеньев и, умножив их на угловую скорость ведущего звена, получить формулы расчета искомых скоростей.

Для решения задачи об ускорениях находят также аналоги ускорений звеньев и по формулам, приведенным в таблице, находят величины ускорений. Ниже приводится пример кинематического анализа кривошипно-ползунного механизма аналитическим методом.