Метрические пространства
Напомним некоторые определения, понятия и результаты, возможно, известные из курса анализа.
Метрическое пространство – этопроизвольное непустое множество E с заданным на нём отображением r : E ® R, называемым метрикой и удовлетворяющим следующим трём свойствам:
неотрицательность: " x , y Î E r(x, y) ³ 0 Ù (r(x, y) = 0 « x = y),
симметричность: " x, y Î E r(x, y) = r(y, x),
неравенство треугольника: " x , y, z Î E r(x, z) £ r(x, y) + r(y, z). Величину r(x, y) называют также расстоянием между точками x, y метрического пространства E.
Примеры: 1.На числовой оси Rопределено обычное расстояние r(x, y) = |x – y|, превращающее Rв метрическое пространство.
2. В пространстве Rn определено обычное расстояние, превращающее Rnв метрическое пространство: для x = (x1 ; … ; xn), y = (y1 ; … ; yn) Î Rn положим r(x, y) = 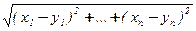 .
.
3. На любом множестве E ¹ Æ можно задать тривиальную метрику r(x, y) = 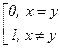 . Ясно, что все свойства метрики выполнены.
. Ясно, что все свойства метрики выполнены.
4. Уже из предыдущих примеров видно, что одно и то же множество можно превратить в метрическое пространство разными способами, задавая на нём разные метрики. Например, на Rn метрикой будет и отображение r(x, y) = = 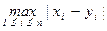 .
.
5. На множестве F([0; 1], R) всех непрерывных функций, определённых на [0; 1], со значениями в R метрикой будет r(f, g) = 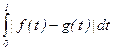 .
.
В метрическом пространстве можно ввести понятие сходимости последовательности. Последовательность {xn}n Î N называется сходящейся к пределу x Î E, если " e > 0 ($ N Î N (" n ³ N r(xn , x) < e)). В этом случае пишут x = 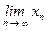 . Это определение согласуется с обычным школьным определением сходимости числовых последовательностей.
. Это определение согласуется с обычным школьным определением сходимости числовых последовательностей.
По аналогии с пространством Rn в произвольном метрическом пространстве можно ввести понятие непрерывной функции: если есть два метрических пространства (E1 , r1), (E2 , r2) , функция f : E1 ® E2 называется непрерывной в точке x0 из области определения D(f) функции f , если " e > 0 $ d > 0 " x Î D(f) (r(x, x0) < d) ® (r(f(x), f(x0)) < e). Функция f, определённая на множестве M, называется непрерывной на M, если она непрерывна в каждой точке множества M.
Полностью аналогично известным определениям вводится понятие непрерывности функции нескольких аргументов f : E1´ … ´En ® E в точке области её определения (y1 ; … ; yn) Î D(f) Í E1´ … ´En :
" e > 0 $ d > 0 " (x1 ; … ; xn) Î D(f) Í E1´ … ´En
(r1(x1 , y1) < d) Ù … Ù (rn(xn , yn) < d) ® (r(f(x1 , … , xn), f(y1 , … , yn)) < e)
и непрерывной функции на множестве.
Простейшим примером непрерывной функции может служить сама метрика r : E´E ® R :
" e > 0 $ d > 0 " x1 , x2 Î E (r(x1 , y1) < d) Ù (r(x2 , y2) < d) ®
® (|r(x1 , x2) – r(y1 , y2)| < e).
Действительно, по неравенству треугольника, если r(x1 , x2) ³ r(y1 , y2), то r(x1 , x2) £ r(x1 , y1) + r(y1 , x2) £ r(x1 , y1) + r(y1 , y2) + r(y2 , x2), т.е. выполняется 0 £ r(x1 , x2) – r(y1 , y2) £ r(x1 , y1) + r(y2 , x2) < 2×d, так что по заданному e > 0 можно выбрать d = e / 2. Что изменится, если r(x1 , x2) < r(y1 , y2) ?
Другой пример непрерывных функций дают сжимающие отображения: отображение f : E ® E называется сжимающим, если $ c Î [0; 1) " x, y Î E r(f(x), f(y)) £ c·r(x, y). Для получения оценки r(f(x), f(y)) < e достаточно выбрать d = e / c : r(f(x), f(y)) £ c·r(x, y) < c×(e / c) = e.
Последовательность {xn}n Î N называется фундаментальной или последовательностью Коши, если
" e > 0 ($ N Î N (" n, m ³ N r(xn , xm) < e)).
Метрическое пространство называется полным, если в нём любая фундаментальная последовательность сходится.
Примеры: 1. Пространство Rnс рассмотренными выше метриками r(x, y) = 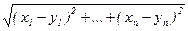 или r(x, y) =
или r(x, y) = 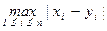 полно.
полно.
2. Метрическое пространство с тривиальной метрикой полно, т.к. любая последовательность Коши в нём имеет бесконечный “хвост” из одного и того же элемента, к которому и сходится: если {xn}n Î N – последовательность Коши, то взяв e = 0,5 из условия $ N Î N (" n, m ³ N r(xn , xm) < 0,5) и тривиальности метрики, получим xn = xm , т.е. рассматриваемая последовательность имеет вид x1 , x2 , … , xN–1 , x, x, …. Элемент x будет её пределом (?!).
3. Пространство Q рациональных чисел с метрикой r(x, y) = |x – y| полным не будет. Для указания не сходящейся фундаментальной последовательности можно, например, взять бесконечную десятичную дробь
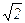 = 1,4142135623730950488016887242097…
= 1,4142135623730950488016887242097…
и задать последовательность {xn}n Î N , беря за xn конечную десятичную дробь, состоящую из первых n цифр указанного бесконечного десятичного разложения иррационального числа 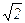 : x1 = 1, x2 = 1,4 =
: x1 = 1, x2 = 1,4 = 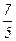 , x3 = 1,41 =
, x3 = 1,41 = 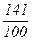 и т.д. Эта последовательность будет фундаментальной: какое бы e ни взять, можно найти N со свойством 10–N+1 < e , и члены последовательности xn , xm при n ³ m ³ N будут иметь m первых одинаковых цифр, т.е.
и т.д. Эта последовательность будет фундаментальной: какое бы e ни взять, можно найти N со свойством 10–N+1 < e , и члены последовательности xn , xm при n ³ m ³ N будут иметь m первых одинаковых цифр, т.е.
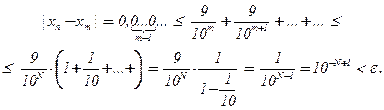
Таким образом, эта фундаментальная последовательность не имеет предела в Q, хотя и сходится к 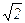 в R.
в R.
4. Пространство F([0; 1], R) всех непрерывных функций, определённых на [0; 1] , со значениями в R и метрикой r(f, g) = 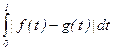 тоже не будет полным. Это следует из того, что любую (не обязательно непрерывную функцию) можно сколь угодно близко (по этой метрике) приблизить полиномами. Таким образом, можно построить фундаментальную последовательность полиномов, не имеющую предела в классе непрерывных функций.
тоже не будет полным. Это следует из того, что любую (не обязательно непрерывную функцию) можно сколь угодно близко (по этой метрике) приблизить полиномами. Таким образом, можно построить фундаментальную последовательность полиномов, не имеющую предела в классе непрерывных функций.
Важность рассмотрения полных метрических пространств обусловлена, в частности, следующей теоремой:
Теорема (о неподвижной точке сжимающего отображения). Пусть в полном метрическом пространстве E c метрикой r определено сжимающее отображение f : E ® E (т.е. отображение со свойством $ c Î [0; 1) " x, y Î E r(f(x), f(y)) £ c·r(x, y)). Тогда у f существует единственная неподвижная точка x Î E: f(x) = x. Эта неподвижная точка может быть получена, например, как предел последовательности {xn}n Î N , где x1 = f(x0), xn+1 = f(xn), а x0 – произвольный элемент из E. При этом r(x, xn) £ 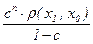 и r(xn+1 , x) £ c·r(xn , x).
и r(xn+1 , x) £ c·r(xn , x).
Доказательство. Пусть x0 Î E , x1 = f(x0), xn+1 = f(xn) (n Î N). Докажем, что эта последовательность фундаментальна, а потому и сходящаяся в полном метрическом пространстве E.
По неравенству треугольника при n ³ m имеем
r(xn , xm) £ r(xn , xn–1) + r(xn–1 , xm) £ r(xn , xn–1) + r(xn–1 , xn–2) + r(xn–2 , xm) £ £ … £ r(xn , xn–1) + r(xn–1 , xn–2) + … + r(xm+1 , xm).
Ввиду сжимаемости рассматриваемого отображения верны неравенства
r(xi , xi–1) = r(f(xi–1), f(xi–2)) £ c·r(xi–1 , xi–2) £
£ c2·r(xi–2 , xi–3) £ … £ ci–1·r(x1 , x0 ).
Значит, из предыдущего получаем
r(xn , xm) £ r(xn , xn–1) + r(xn–1 , xn–2) + … + r(xm+1 , xm) £
£ cn–1·r(x1 , x0 ) + cn–2·r(x1 , x0 ) + … + cm·r(x1 , x0 ) £
£ 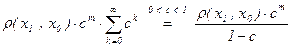 .
.
Если x1 = x0 , т.е. r(x1 , x0 ) = 0, то доказывать нечего: x0 – неподвижная точка. В случае r(x1 , x0 ) ¹ 0 для любого e > 0 можно найти N Î Nсо свойством cN < 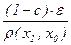 , положив
, положив 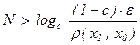 . Поэтому при n ³ m ³ N получим оценку r(xn , xm) £
. Поэтому при n ³ m ³ N получим оценку r(xn , xm) £ 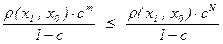 < e .
< e .
Итак, последовательность {xn}n Î N фундаментальна, и (ввиду полноты пространства E) существует x = 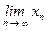 Î E. Соотношение xn+1 = f(xn) при n ® ¥ даёт (ввиду непрерывности функции f )равенство x = f(x), т.е. x – неподвижная точка отображения f . Эта неподвижная точка единственна: если y – ещё одна неподвижная точка, то из условия сжимаемости получим r(x, y) = r(f(x), f(y)) £ c·r(x, y) < r(x, y) – противоречие.
Î E. Соотношение xn+1 = f(xn) при n ® ¥ даёт (ввиду непрерывности функции f )равенство x = f(x), т.е. x – неподвижная точка отображения f . Эта неподвижная точка единственна: если y – ещё одна неподвижная точка, то из условия сжимаемости получим r(x, y) = r(f(x), f(y)) £ c·r(x, y) < r(x, y) – противоречие.
Перейдя в неравенстве 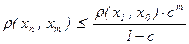 к пределу при n ® ¥, получим требуемую оценку
к пределу при n ® ¥, получим требуемую оценку 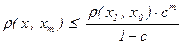 . Кроме того, из условия сжимаемости r(xn+1 , xm+1) = r(f(xn), f(xm)) £ c·r(xn , xm) в пределе при m ® ¥ следует неравенство r(xn+1 , x) £ c·r(xn , x).
. Кроме того, из условия сжимаемости r(xn+1 , xm+1) = r(f(xn), f(xm)) £ c·r(xn , xm) в пределе при m ® ¥ следует неравенство r(xn+1 , x) £ c·r(xn , x).
Теорема доказана.
Частным случаем метрического пространства является нормированное векторное пространство – это векторное пространство V над полем R c заданной нормой ||·|| : V ® R, удовлетворяющей свойствам:
неотрицательность: " x, y Î V||x|| ³ 0 Ù (||x|| = 0 « x = 0),
однородность: " l Î R " x Î V||l·x|| = |l|·||x||,
неравенство треугольника: " x, y Î V||x + y|| £ ||x|| + ||y||.
Примеры: 1. На пространстве Rn можно задать следующие нормы ||x||2 = 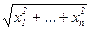 , ||x||¥ =
, ||x||¥ = 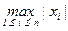 , ||x||1 =
, ||x||1 = 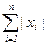 . Легко понять, что ||x||¥ £ ||x||2 £ ||x||1 £ n·||x||¥ .
. Легко понять, что ||x||¥ £ ||x||2 £ ||x||1 £ n·||x||¥ .
2. Любое нормированное векторное пространство V с нормой ||·|| можно превратить в метрическое пространство, задав индуцированную метрику формулой r(x, y) = ||x – y||.
3. На множестве F([0; 1], R) всех непрерывных функций, определённых на [0; 1] , со значениями в R нормой будет || f || = 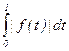 .
.
Поскольку нормированное пространство является метрическим, то в нём определяются понятия сходимости, которые для удобства читателя сформулируем в терминах нормы. Последовательность {xn}n Î N называется сходящейся к пределу x Î V : x = 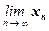 , если " e > 0 ($ N Î N (" n ³ N ||xn – x|| < e)). Последовательность {xn}n Î N называется фундаментальной или последовательностью Коши, если " e > 0 ($ N Î N (" n, m ³ N ||xn – xm|| < e)). Нормированное пространство называется полным, если в нём любая фундаментальная последовательность сходится. Полные нормированные пространства называют также банаховыми. Ясно, что нормированное пространство V с нормой ||·|| будет банаховым тогда и только тогда, когда оно полно относительно индуцированной метрики r(x, y) = ||x –y||.
, если " e > 0 ($ N Î N (" n ³ N ||xn – x|| < e)). Последовательность {xn}n Î N называется фундаментальной или последовательностью Коши, если " e > 0 ($ N Î N (" n, m ³ N ||xn – xm|| < e)). Нормированное пространство называется полным, если в нём любая фундаментальная последовательность сходится. Полные нормированные пространства называют также банаховыми. Ясно, что нормированное пространство V с нормой ||·|| будет банаховым тогда и только тогда, когда оно полно относительно индуцированной метрики r(x, y) = ||x –y||.
Две нормы ||·||1 и ||·||2 на векторном пространстве V называются эквивалентными, если существуют константы m , M Î R со свойствами " x Î V m·||x||1 £ ||x||2 £ M·||x||1 . Выше в примере 1 были приведены неравенства, показывающие эквивалентность норм ||x||¥ ,||x||2 ,||x||1 .
Упомянем без доказательства следующую важную теорему:
Теорема (об эквивалентности норм в Rn ). Любые две нормы в пространстве Rn эквивалентны. Это означает, что любые нормы в Rn определяют одну и ту же топологию: последовательности, сходящиеся по какой-то одной норме, сходятся и по другим нормам.
Матричные нормы
Множество M(n, R) всех квадратных n´n-матриц над полем действительных чисел, как известно, образует векторное пространство размерности n2, которое можно отождествить с R 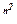 . Поэтому можно определить следующие нормы на M(n, R):
. Поэтому можно определить следующие нормы на M(n, R):
||A||2 = 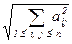 , ||A||¥ =
, ||A||¥ = 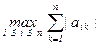 , ||A||1 =
, ||A||1 = 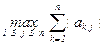 ,
,
где A = (aij) – квадратная n´n-матрица с компонентами aij (1 £ 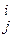 £ n). Вопрос о том, почему эти нормы обозначены аналогично введённым выше векторным нормам, но некоторые из них выглядят иначе, будет обсуждаться позднее.
£ n). Вопрос о том, почему эти нормы обозначены аналогично введённым выше векторным нормам, но некоторые из них выглядят иначе, будет обсуждаться позднее.
Примеры: 1. Для матрицы A = 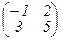 получаем
получаем
||A||2 = 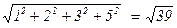 , ||A||¥ = max{|–1| + |2|, |3| + |5| } = 3,
, ||A||¥ = max{|–1| + |2|, |3| + |5| } = 3,
||A||1 = max{|–1| + |3|, |2| + |5|} = 4.
2. Для единичной матрицы I = 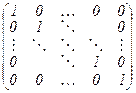 любого порядка значения всех рассматриваемых норм равны 1.
любого порядка значения всех рассматриваемых норм равны 1.
Оказывается, что эти нормы, определённые для матриц в векторном пространстве, тесно связаны с умножением матриц: " A, B Î M(n, R) ||A·B|| £ ||A||·||B||.
Это легко проверить для ||·||¥ : если C = A·B, то cij = 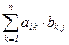 и
и 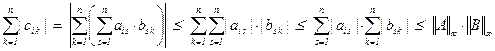 . Поэтому ||C||¥ =
. Поэтому ||C||¥ = 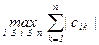 £ ||A||¥ ·||B||¥ .
£ ||A||¥ ·||B||¥ .
Для нормы ||·||1 вычисления аналогичны. В случае ||·||2 нужно проверить неравенство 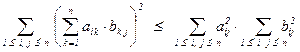 , справедливость которого можно уяснить, воспользовавшись неравенством Коши-Буняковского-Шварца – модуль скалярного произведения векторов не превосходит произведения их длин:
, справедливость которого можно уяснить, воспользовавшись неравенством Коши-Буняковского-Шварца – модуль скалярного произведения векторов не превосходит произведения их длин: 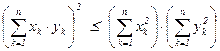 . Поэтому
. Поэтому
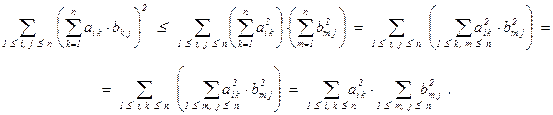
Есть другой, более общий, подход к определению матричных норм. Если задана некоторая векторная норма ||·|| в векторном пространстве nR всех столбцов длины n, то единообразно можно определить связанную с ней матричную норму ||A|| = sup{||A·x|| Î R | x Î nR , ||x|| = 1}. Этот супремум конечен, т.к. множество {x Î nR | ||x|| = 1} ограничено и замкнуто, так что непрерывная функция ||A·x|| на нём достигает максимума.
Теорема (о матричной норме). Если в пространстве nR задана норма ||·|| , то формула ||A|| = sup{||A·x|| Î R| x Î nR , ||x|| = 1} определяет матричную норму, т.е. отображение ||·|| : M(n, R) ® R со свойствами:
(Н1): " A Î M(n, R) ||A|| ³ 0 Ù (||A|| = 0 « A = 0)
(Н2): " l Î R " A Î M(n, R) ||l·A|| = |l|·||A||
(Н3): " A, B Î M(n, R) ||A + B|| £ ||A|| + ||B||
(Н4): " A, B Î M(n, R) ||A·B|| £ ||A||·||B||.
При этом " x Î nR||A·x|| £ ||A||·||x||.
Доказательство. Для краткости будем писать sup{||A·x||} вместо sup{||A·x|| Î R | x Î nR , ||x|| = 1}.
(Н1): Условие ||A|| ³ 0 очевидно. Кроме того,
(||A|| = 0) Û (sup{||A·x||} = 0) Û (" x Î nR||A·x|| = 0) Û
Û (" x Î nR A·x = 0) Û A = 0.
(Н2): ||l·A|| = sup{||l·A·x||} = sup{|l|·||A·x||} = |l|·sup{||A·x||} = |l|·||A||.
(Н3): ||A + B|| = sup{||(A + B)·x||} = sup{||A·x+B·x||} £ sup{||A·x|| + ||B·x||} £ £ sup{||A·x||} + sup{||B·x||} = ||A|| + ||B||.
Докажем теперь неравенство " x Î nR||A·x|| £ ||A||·||x||. Оно очевидно для x = 0. Еслиx ¹ 0, то для y = 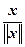 имеем ||y|| =
имеем ||y|| = 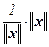 = 1, поэтому ||A|| = sup{||A·z|| | ||z|| = 1} ³ ||A·y|| =
= 1, поэтому ||A|| = sup{||A·z|| | ||z|| = 1} ³ ||A·y|| = 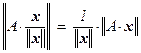 , откуда и следует, что ||A·x|| £ ||A||·||x|| .
, откуда и следует, что ||A·x|| £ ||A||·||x|| .
(Н4): ||A·B|| = sup{||(A·B)·x||} = sup{||A·(B·x)||} £ sup{||A||·||B·x||} = = ||A||·sup{||B·x||} £ ||A||·sup{||B||·||x||} = ||A||·||B||·sup{||x|| | ||x|| = 1} = ||A||·||B||.
Теорема доказана.
Упражнения: 1.Докажите, что по любой матричной норме можно построить векторную норму: именно по ||·|| : M(n, R) ® Rопределяется норма ||·|| : nR ® R по правилу ||x|| = ||(x … x)||, где (x … x) Î M(n, R) – матрица, полученная n-кратным повторением столбца x Î nR.
2. Докажите, что модуль |l| Î R любого собственного числа матрицы A Î M(n, R) не превосходит произвольной нормы ||A|| матрицы A.
3. Докажите, что формула
||A|| = max{|l| Î R | l Î C – собственное число матрицы А}
Определяет матричную норму.
Оказывается, что описанным в теореме о матричных нормах путём по нормам ||·||2 , ||·||¥ и ||·||1 в nR можно получить рассмотренные выше соответствующие нормы матриц. Доказывать это не будем.
Ввиду тесной связи нормы ||·|| в банаховом пространстве с индуцированной метрикой r(x, y) = ||x – y|| теорему о неподвижной точке сжимающего отображения можно переформулировать и для банаховых пространств:
Теорема (о неподвижной точке сжимающего отображения). Пусть в банаховом пространстве B с нормой ||·|| определено сжимающее отображение f : B ® B, т.е. $ c Î [0; 1) " x, y Î B ||f(x) – f(y)|| £ c·||x – y|| . Тогда у него существует единственная неподвижная точка x Î B: f(x) = x. Эта неподвижная точка может быть получена, например, как предел последовательности {xn}n Î N , где x1 = f(x0), xn+1 = f(xn), а x0 – произвольный элемент из B. При этом || xn+1 – x || £ c·|| xn – x || , || x – xn || £ 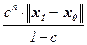 .
.
Важным для приложений является случай сжимающего линейного оператора, т.е. сжимающего отображения f : B ® B, удовлетворяющего условию линейности " a, b Î R " x, y Î B f(a·x + b·y) = a·f(x) + b·f(y).
Теорема (о сжимающих линейных операторах). Линейный оператор f : B ® B является сжимающим тогда и только тогда, когда $ с Î [0; 1) " x Î B ||f(x)|| £ c·||x||. Сжимающий линейный оператор имеет единственную неподвижную точку: 0 Î B. Если f – сжимающий линейный оператор, то линейный оператор e – f : B ® B, где e – тождественное отображение, инъективен.
Доказательство. Если оператор сжимающий, то при y = 0 из условия сжимаемости получим ||f(x) – f(0)|| £ c·||x – 0||, т.е. ||f(x)|| £ c·||x||. Обратно, если " x Î B ||f(x)|| £ c·||x||, то при x = y – zбудет верно " y , z Î B ||f(y) – f(z)|| = ||f(y – z)|| £ c·||y – z || , что и требовалось.
Очевидно, что 0 – неподвижная точка линейного оператора: f(0) = 0. Если сжимающий линейный оператор имеет неподвижную точку x, то f(x) = x, и ||x|| = ||f(x)|| £ c·||x||, что при x ¹ 0 приводит к противоречию 1 £ c. Поэтому x = 0– единственная неподвижная точка оператора f.
По определению, " x Î B (e – f)(x) = x – f(x). Предположим, что (e – f)(x) = (e – f)(y), т.е. x – f(x) = y – f(y) или x – y = f(x) – f(y) = f(x – y). Значит, x – y – неподвижная точка сжимающего оператора, и поэтому, x – y = 0 , т.е. x = y.
Теорема доказана.
Замечание: Вообще говоря, для бесконечномерного банахова пространства B в условиях теоремы линейный оператор e – f : B ® B не обязан быть сюръективным.
Если B = Rn, то, как известно из курса алгебры, инъективность линейного оператора равносильна его обратимости, т.е. из инъективности оператора в конечномерном пространстве следует его сюръективность. Поэтому получаем
Следствие (об обратимости матрицы). Пусть А Î M(n, R) и ||A|| < 1. Тогда матрица In – A обратима.
Доказательство. Рассмотрим линейный оператор j : nR ® nR, определённый правилом j(x) = A·x. Это – линейный оператор с матрицей A относительно стандартного базиса e1 , … , enпространства nR , где ei = (0; … ; 0; 1; 0; … ; 0)t – вектор-столбец с единицей на i-м месте и нулями на остальных. Этот оператор будет сжимающим: " x Î nR||j(x)|| = ||A·x|| £ ||A||·||x||и ||A|| < 1, так что в условии сжимаемости оператора j можно взять c = ||A|| Î [0; 1). По теореме о сжимающих линейных операторах, оператор e – j обратим. Его матрицей в стандартном базисе e1 , … , en будет In – A, что и доказывает её обратимость.
Лемма доказана.
Примеры: 1. Для матрицы A = 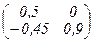 имеем
имеем
||A||2 = 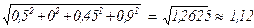 ,
,
||A||¥ = max{|0,5| + |0|, |–0,45| + |0,9|} = 1,35,
||A||1 = max{|0,5| + |–0,45|, |0| + |0,9|} = 0,95 < 1.
Таким образом, матрица I – A = 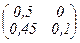 обратима. Об этом свидетельствует неравенство нулю её определителя и ||A||1 . Остальные нормы не позволяют сделать вывод об обратимости матрицы I – A.
обратима. Об этом свидетельствует неравенство нулю её определителя и ||A||1 . Остальные нормы не позволяют сделать вывод об обратимости матрицы I – A.
2. Для матрицы A = 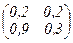 имеем
имеем
||A||2 = 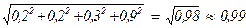 < 1,
< 1,
||A||¥ = max{|0,2| + |0,2|, |0,9| + |0,3|} = 1,2,
||A||1 = max{|0,2| + |0,9|, |0,2| + |0,3|} = 1,1.
Таким образом, матрица I – A = 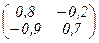 обратима. Об этом свидетельствует неравенство нулю её определителя и ||A||2 . Остальные нормы не позволяют сделать вывод об обратимости матрицы I – A.
обратима. Об этом свидетельствует неравенство нулю её определителя и ||A||2 . Остальные нормы не позволяют сделать вывод об обратимости матрицы I – A.
Эти примеры показывают, что для решения задач полезно использовать весь спектр норм: некоторые не помогут, но возможно, какая-то из них и облегчит решение задачи.
Дата добавления: 2021-12-14; просмотров: 384;











