Ортогональные дополнения подпространств евклидова пространства
Пусть U, W – два подпространства в векторном пространстве V, причем U Ç W = {0} и " v Î V $ u Î U , w Î Wv = u + w, т.е. V = U + W. Тогда говорят, что пространство V является прямой суммой подпространств U и W и пишут V = U Å W.
Примеры: 1. Пусть V = V2(O, R) – множество всех векторов плоскости, отложенных от т. О, и на плоскости задана аффинная система координат с центром в т. О, U = { u Î V | uлежит на оси ОХ }, W= { w Î V | wлежит на оси ОY }.Тогда V = U Å W (?!).
2. Пусть V = R3. Рассмотрим подпространства
U = {(u1 ; u2 ; u3) Î R3 | u1 + u2 + u3 = 0}, W = {(w1 ; w2 ; w3) Î R3 | w1 = w2 = 0}
(почему они будут подпространствами в V ?!). Тогда V = U Å W. Действительно, если v = (v1 ; v2 ; v3) Î U Ç W, то 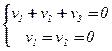 , т.е. v1 = v2 = = v3 = 0, и U Ç W = {0}. Справедливость равенства U + W = V следует из представления (v1 ; v2 ; v3) = (v1 ; v2 ; –v1 – v2) + (0; 0; v3 + v1 + v2) Î U + W.
, т.е. v1 = v2 = = v3 = 0, и U Ç W = {0}. Справедливость равенства U + W = V следует из представления (v1 ; v2 ; v3) = (v1 ; v2 ; –v1 – v2) + (0; 0; v3 + v1 + v2) Î U + W.
Упражнение.Докажите, что (V = U Å W) Û (" v Î V $ ! u Î U, w Î Wv = u + w).
Теорема (об ортогональном дополнении). Пусть (V, (_, _)) – евклидово пространство, U – его конечномерное подпространство. Тогда
U^= {w Î V | " u Î U (u , w) = 0 }
является подпространством в V, причем V = U Å U^. Пространство U^ называется ортогональным дополнением к U в пространстве V.
Доказательство. Прежде всего, U^¹ Æ, т.к. 0 Î U^. Кроме того, U^ замкнуто относительно сложения и умножения на скаляры. В самом деле, если w1 , w2 Î U^, a Î R, то для любого u Î U имеем:
(u, w1 + w2) = (u, w1)+(u, w2) = 0+0 = 0, (u, a×w1) = a×(u,w 1) = a×0 = 0.
По лемме о подпространстве, U^ – подпространство в V.
Докажем, что V = U Å U^. Пусть v Î U Ç U^. Тогда по определению U^ имеем (v , v) = 0, и v = 0 из неотрицательности скалярного произведения. Итак, U Ç 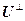 = {0}. Осталось проверить, что V = U + U^. Если U = {0}, то U^ = V, и доказывать нечего. Если же U ¹ {0}, то (по теореме об ортонормированном базисе) можно выбрать ортонормированный базис e = (e1 , … , en ) в U. Пусть v Î Vиu = (v , e1 )×e1 + … + (v , en)×en Î U, g = v – u. Тогда,как и в теореме об ортонормированном базисе, убеждаемся, что g ^ ei (1 £ i £ n), т.е. g Î U^ (?!) и v = u + g Î U + U^.
= {0}. Осталось проверить, что V = U + U^. Если U = {0}, то U^ = V, и доказывать нечего. Если же U ¹ {0}, то (по теореме об ортонормированном базисе) можно выбрать ортонормированный базис e = (e1 , … , en ) в U. Пусть v Î Vиu = (v , e1 )×e1 + … + (v , en)×en Î U, g = v – u. Тогда,как и в теореме об ортонормированном базисе, убеждаемся, что g ^ ei (1 £ i £ n), т.е. g Î U^ (?!) и v = u + g Î U + U^.
Теорема доказана.
Примеры: 1. Найти ортогональное дополнение к подпространству U, порожденному векторами u1 = (0; 1; –1; 1) и u2 = (–1; 0; 0; 1) стандартного евклидова пространства R4.
Так как U^ = {w Î R4 | " u Î U (u , w) = 0 }, то
((w1 ; w2 ; w3 ; w4) Î 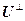 ) Û
) Û 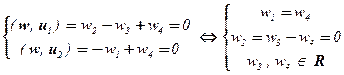 .
.
Таким образом, U^ = { (w4 ; w3 – w4 ; w3 ; w4) Î R4 | w3 , w4 Î R }. Базисом 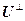 является фундаментальная система решений рассмотренной однородной системы линейных уравнений, получающаяся из найденного общего решения при значениях свободных переменных w3 = 1, w4 = 0 и w3 = 0, w4 = 1 – а именно система векторов (0; 1; 1; 0), (1; –1; 0; 1).
является фундаментальная система решений рассмотренной однородной системы линейных уравнений, получающаяся из найденного общего решения при значениях свободных переменных w3 = 1, w4 = 0 и w3 = 0, w4 = 1 – а именно система векторов (0; 1; 1; 0), (1; –1; 0; 1).
2. Пусть V = V2(O, R) со стандартным скалярным произведением (a , b) = = |a|×|b|×cos(Ð a ,b). Если U = { u Î V | u лежит на прямой y = 2×x }, то легко доказать, что U^= { w Î V | w лежит на прямой y = – 0,5×x } (?!).
Симметричные линейные операторы
Квадратная матрица A порядка n над полем F называется симметричной, если At = A. Линейный оператор h: Fn 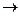 Fnназывается симметричным, если его матрица в стандартном базисе симметрична. Нашей целью является доказательство следующей важной теоремы:
Fnназывается симметричным, если его матрица в стандартном базисе симметрична. Нашей целью является доказательство следующей важной теоремы:
Теорема (о спектре симметричного линейного оператора). Собственные числа симметричного оператора h: Rn 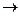 Rnвещественны, а его матрица диагонализируема (по диагонали стоят собственные числа).
Rnвещественны, а его матрица диагонализируема (по диагонали стоят собственные числа).
Доказательство.Пусть A – матрица симметричного оператора h в стандартном базисе, l = m + i×n – её (возможно, комплексное) собственное значение (m, n 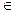 R), а z – соответствующий ему собственный вектор с (возможно, комплексными) компонентами zk = xk + i×yk (xk , yk Î R, 1 £ k £ n). Тогда z = x+ i×y, гдеx, y – вещественные векторы с компонентами xk , yk Î R, (1 £ k £ n). Задумайтесь: почему у матрицы A есть хотя бы одно собственное число и собственный вектор ?
R), а z – соответствующий ему собственный вектор с (возможно, комплексными) компонентами zk = xk + i×yk (xk , yk Î R, 1 £ k £ n). Тогда z = x+ i×y, гдеx, y – вещественные векторы с компонентами xk , yk Î R, (1 £ k £ n). Задумайтесь: почему у матрицы A есть хотя бы одно собственное число и собственный вектор ?
Так как A×z = l×z , то A×(x+ i×y) = (m+ i×n)×(x+ i×y). Учитывая, что A вещественная матрица, и сравнивая действительные и мнимые части в полученном равенстве, приходим к двум условиям: A×x = m×x – n×y, A×y = m×y + n×x . При этом (A×y = m×y +n×x) Û ((A×y)t = (m×y + n×x)t) Û (yt×At = (m×yt + n×xt)). Учитывая, что At = A,получаем систему 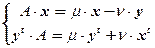 . Умножая первое уравнение на yt слева, а второе – на xсправа, и вычитая одно из другого, приходим к равенству
. Умножая первое уравнение на yt слева, а второе – на xсправа, и вычитая одно из другого, приходим к равенству
0 = –n×yt×y – n×xt×x = –n×(y12 + … + yn2 + x12 + … + xn2).
Отсюда либо n = 0, либо y1 = … = yn = x1 = … = xn = 0. Последняя возможность исключается, т.к. собственный вектор z = x+ i×yненулевой, и, значит, n = 0. Итак, 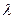 Î R .
Î R .
Для доказательства диагонализируемости матрицы A проведем индукцию по n и докажем, что существует такая ортогональная матрица S, что матрица S –1×A×S = D диагональна с собственными числами матрицы A по диагонали (ортогональность матрицы S означает, что S –1 = S t – транспонированная матрица).При этом будем рассматривать пространство nRкак евклидово со стандартным скалярным произведением (x, y) = xt×y .
База индукции (n = 1) очевидна. Предположим, что любая симметричная матрица порядка n – 1 диагонализируема с собственными числами по диагонали, и докажем это для матрицы A порядка n. Пусть l – одно из её собственных чисел (которые, по доказанному выше, все вещественны), а x – соответствующий собственный вектор с вещественными (?!) компонентами и U = L(x) – одномерное подпространство в nR , натянутое на векторx. По теореме об ортогональном дополненииподпространства имеем nR = U Å U^, где U^ = { y Î nR | xt×y = 0 }.
Заметим, что " y Î U^ A×y Î U^. Действительно,xt×A×y = (?!) = (A×x)t×y = = (l×x)t×y = l×xt×y = 0. Таким образом, если f1 , … , fn–1 – ортонормированный базис пространства U^ , то A×fi = 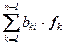 .Это значит, что в базисе e = (x, f1 , … , fn–1) матрица [h]eраспавшаяся:
.Это значит, что в базисе e = (x, f1 , … , fn–1) матрица [h]eраспавшаяся:
[h]e = T –1×A×T = 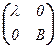 ,
,
где B = (bij) Î M(n–1, F), T = ( 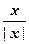 , f1 , … , fn ), T –1 = T t . При этом полученная матрица снова симметрична:
, f1 , … , fn ), T –1 = T t . При этом полученная матрица снова симметрична:
(T –1×A×T)t = (T t×A×T)t = T t×A t×(T t)t = T t×A×T = T –1×A×T.
В частности, симметрична матрица B, к которой применимо предположение индукции.
По предположению индукции, B = P –1×d×P, где P –1 = P t , d – диагональная матрица с собственными числами матрицы B по диагонали, так что
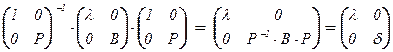
– диагональная матрица с собственными числами матрицы A по диагонали (?!). В итоге 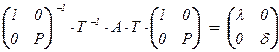 , где сопрягающая матрица T×
, где сопрягающая матрица T× 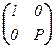 ортогональна:
ортогональна:
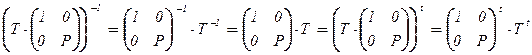 .
.
Теорема доказана.
Примеры: 1. Если h : R2 ® R2 , где h(x, y) = (x + y ; x + y), то в стандартном базисе [h]e = A = 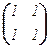 . Для нахождения её диагональной формы найдём собственные числа и собственные векторы.
. Для нахождения её диагональной формы найдём собственные числа и собственные векторы.
1. Решаем характеристическое уравнение:
|l×I2 – A| = 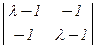 = (l – 1)2 – 1 = (l – 2)×l = 0.
= (l – 1)2 – 1 = (l – 2)×l = 0.
Таким образом, l1 = 2, l2 = 0.
2. Находим собственные векторы, решая системы (li×I2 – A)×v = 0 (i = 1, 2).
а) l1 = 2: 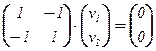 Û
Û 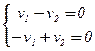 Û v =
Û v = 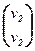 , v2 ¹ 0.
, v2 ¹ 0.
б) l2 = 0: 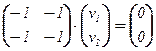 Û
Û 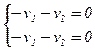 Û v =
Û v = 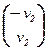 , v2 ¹ 0.
, v2 ¹ 0.
3. Находим базис из собственных векторов и нормируем его: b1 = 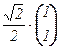 , b2 =
, b2 = 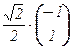
4. Составляем из базисных векторов сопрягающую матрицу:
T = 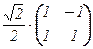 , T –1 = T t =
, T –1 = T t = 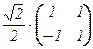 .
.
5. Находим диагональный вид матрицы:
T –1×A×T = 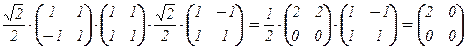 .
.
2. Если h : R3 ® R3 , где
h(x, y, z) = (x + y ; x + y + z ; y + z),
то в стандартном базисе [h]e = A = 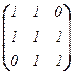 . Для нахождения её диагональной формы найдём собственные числа и собственные векторы.
. Для нахождения её диагональной формы найдём собственные числа и собственные векторы.
1. Решаем характеристическое уравнение:
|l×I3 – A| = 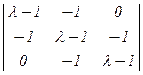 = (l – 1)3 – 2×(l – 1) = (l – 1)×(l2 – 2×l – 1) = 0.
= (l – 1)3 – 2×(l – 1) = (l – 1)×(l2 – 2×l – 1) = 0.
Таким образом, l1 = 1, l2 = 1 + 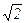 , l3 = 1 –
, l3 = 1 – 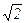 .
.
2. Находим собственные векторы, решая системы (li×I2 – A)×v = 0 (1 £ i £ 3).
а) l1 = 1: 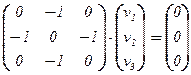 Û
Û 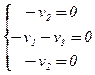 Û v =
Û v =  , v3 ¹ 0.
, v3 ¹ 0.
б) l2 = 1 + 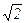 :
: 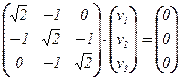 Û
Û 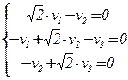 Û v =
Û v = 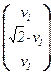 , v1 ¹ 0.
, v1 ¹ 0.
в) l3 = 1 – 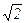 :
: 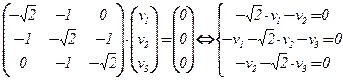 ,v =
,v = 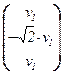 , v1 ¹ 0.
, v1 ¹ 0.
3. Нормированный базис из собственных векторов:
b1 = 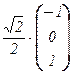 , b2 =
, b2 = 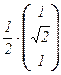 , b3 =
, b3 = 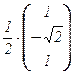 .
.
4. Составляем из базисных векторов сопрягающую матрицу:
T = 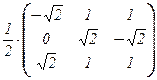 , T –1 = T t =
, T –1 = T t = 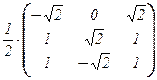 .
.
5. Находим диагональный вид матрицы:
T –1×A×T = 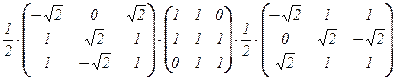 =
=
= 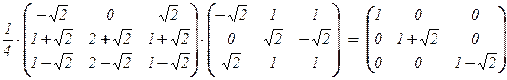 .
.
Дата добавления: 2021-12-14; просмотров: 386;











