Определение и простейшие свойства

Пусть (V , +, {a× | a Î F} ) и (W , Å , {aÄ | a Î F} ) – два векторных пространства над одним и тем же полем F. Любой гомоморфизм векторных пространств j : V ® W называют линейным оператором из (векторного пространства) Vв (векторное пространство) W. Таким образом, j – линейный оператор, если он сохраняет операции сложения и умножения на скаляры, т.е. одновременно выполнены следующие условия:

(А): " u, v Î V j(u+v) = j(u)Å j(v) (условие аддитивности),

(О): " a Î F " v Î V j(a×v) = a Ä j(v) (условие однородности).

Инъективный линейный оператор называется вложением (векторных пространств) или мономорфизмом, сюръективный – наложением или эпиморфизмом, а биективный гомоморфизм – изоморфизмом (векторных пространств). Если V = W, то линейный оператор j : V ® Vназывают эндоморфизмом (векторного пространства V), а изоморфизм j : V ® V – автоморфизмом (векторного пространства V).

Примеры: 1. Пусть j : R² ® R²задано правилом j(x; y) = (x – y; –2×x). Докажем, что j изоморфизм векторных пространств. Вначале проверим гомоморфность:

(А): " u, v Î R² j(u+v) = j(u) + j(v)

Пусть u = (a; b), v= (c; d) Î R². Тогда u + v = (a+c; b+d), j(u+v) = = j(a + c; b + d) = ((a + c)–(b + d); –2×(a + c)) = (a – b; –2×a) + (c – d; –2×c) = = j(a, b) + j(c, d) = j(u)+j(v).

(O): " a Î F " v Î R² j(a×v) = a×j(v)

Пусть u = (a; b) Î R², a Î F. Тогда a×u = (a×a; a×b), j(a×u) = j(a×a;a×b) = = (a×a – a×b; –2×a×a) = a×(a – b; –2a) = a×j(u).

Итак, j – гомоморфизм векторных пространств. Выясним, к какому виду гомоморфизмов относится j. Для этого проверим условия инъективности и сюръективности.

Инъективность: " u, v Î R² j(u) = j(v) ® u = v

Пусть u = (a; b), v = (c; d) Î R² и j(u) = j(v), т.е. (a – b; –2×a) = = (c – d; –2×c) . Ясно, что тогда a = c и b = d, т.е. u = v. Значит j – вложение векторных пространств.

Сюръективность: Im(j) = R², т.е." v Î R² $ v Î R² v = j(u)

Пусть v = (c; d) Î R² . Тогда

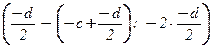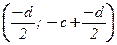v = (c; d) = = j Î Im(j).

Значит j – эпиморфизм векторных пространств.

Итак, j – изоморфизм векторных пространств.

2. Пусть F – поле, V = ⁿ F, A Î M(n, F). Тогда отображение m : ⁿ F ® ⁿ F, заданное правилом " x Î ⁿ F m(x) = A×x является линейным оператором (?!).

3. Если (V, +, {a× | a Î F}) – любое векторное пространство, а W = {0} – нулевое векторное пространство с естественными тривиальными операциями 0 Å 0= 0, " a Î F a Ä 0 = 0, то отображение 0 : V® W , заданное правилом " v Î V 0(v) = 0 будет эпиморфизмом векторных пространств (?!).

4. Если (V, +, {a× | a Î F}) – любое векторное пространство, а W – его подпространство, то тождественное отображение i: W ® V, определённое правилом " w Î W i(w) = w является вложением (?!).

5. Отображение j : R² ® R², заданное правилом j(x; y) = (x + 1; 0) не является линейным оператором, т.к. не удовлетворяет условию аддитивности (?!).

6.Отображение j : R₊ ® R, заданное правилом j(x) = 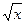не является линейным оператором, т.к. нарушено условие однородности (?!).

7. Пусть V = V₂(O, R), j : V ® V поворачивает любой вектор a Î V на фиксированный угол a против часовой стрелки вокруг т. О (см. рис. 1).

Ясно, что функция j всюду определена на V. Её аддитивность наглядна: если a, b Î V, то их сумма вычисляется по правилу параллелограмма (см. рис. 2). Под действием j весь этот параллелограмм повернётся на угол a , т.е. j(a + b) = j(a) + j(b). Аналогично проверяется свойство однородности. Таким образом, поворот на фиксированный угол a вокруг т. Оявляется эндоморфизмом векторного пространства V₂(O, R). На самом деле отображение j взаимно однозначно (?!), так что j – автоморфизм.

8. Проверьте самостоятельно, что линейным оператором в V₂(O, R) будет и проектирование векторов на фиксированную прямую l, проходящую через т. О, параллельно заданной пересекающей l прямой m. Будет ли этот линейный оператор автоморфизмом ?