Счётные множества и множества мощности континуум

Рассмотрим следующую цепочку числовых множеств N Í Z Í Q Í R Í C и зададим вопрос об эквивалентности этих множеств.

Установим явно взаимно однозначное соответствие между числами множеств Zи N. Выпишем все целые числа … , –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, … и присвоим каждому целому числу некоторый номер. Именно, число 0 получит номер 1, число 1 – номер 2,число –1 – номер 3, и.т.д. Можно даже вычислить номер в общем виде: номер натурального числа n будет равен 2×n, а номер его отрицательного антипода –n будет равен 2×n+1.Таким образом, мы “пересчитаем” все целые числа: каждому zÎ Zсопоставляется некоторое натуральное число (номер) и для каждого номера есть единственное целое число, которому этот номер приписывается.

Таким образом, множество Zэквивалентно множеству N.

Всякое множество X, эквивалентное множеству натуральных чисел, называется счётным и это обозначается так: |X| = À₀ *. В частности, |N| = À₀ . Если множество не является счётным, то говорят, что оно несчётно. Таким образом, множество X несчётно, если не существует взаимно-однозначного (биективного) отображения f : N ® X.

Любое счётное множество можно “пересчитать”: пронумеровать все его элементы натуральными числами: если f : N ® X – взаимно однозначное отображение, то можно представить множество X в виде

X = f(N) = {f(1), … , f(n), …} = {x₁ , … , x_n , …},

где x_n = f(n) – элемент множества X с номером n.

С этой точки зрения счётность множества Z выглядит естественной – ведь множество целых чисел дискретно на числовой прямой. На первый взгляд, рациональных чисел на прямой “намного больше”, чем целых. Они расположены всюду плотно: в любом сколь угодно малом интервале их бесконечно много. Но оказывается, что

ТеоремаМножество рациональных чисел Q счётно.

Доказательство: Сначала докажем счётность множества Q⁺всех положительных рациональных чисел.

Выпишем все элементы Q⁺ таким образом: в первой строке – все числа со знаменателем 1 (т.е. целые), во второй – со знаменателем 2 и т.д. Каждое положительное рациональное число обязательно встретится в этой таблице, и не однажды (например, 1 = 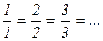встречается в каждой строке).

				…
				…
				…
				…
…	…	…	…	…

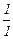
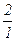
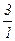
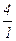
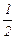
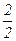
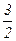
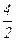
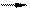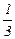
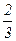
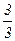
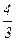
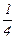
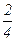
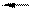
А теперь пересчитаем эти числа, присваивая каждому числу номер (или пропускаем это число, если оно уже встречалось нам раньше в другой записи), двигаясь по зигзагообразной линии, как указано в таблице. Ясно, что мы обойдём всю таблицу (т.е. рано или поздно доберемся до любого из чисел) и каждому положительному рациональному числу присвоим номер. Итак, мы указали способ пронумеровать все числа из Q⁺, т.е. доказали, что Q⁺счётно.

Теперь заметим, что Q = Q⁺ È {0} È Q^– , где Q^– – множество всех отрицательных рациональных чисел. Поэтому для нумерации всех рациональных чисел можно применить приём, использованный при нумерации целых чисел. Именно, номер 1 присвоим рациональному числу 0, номер 2 = 2×1 – положительному рациональному числу с номером 1, а номер 3 = 2×1+1 – противоположному ему отрицательному числу, и т.д. Таким образом, номер 2×n получит n-е число q_n из Q⁺, а номер 2×n+1 – отрицательное число –q_n Î Q^–.

Теорема доказана.

Сразу ответим на естественный вопрос: существуют ли несчётные множества ?

Теорема (о несчётности множеств R и [0; 1]).Множества R и [0; 1] несчётны.

Доказательство.Рассуждения для множеств R и [0; 1] проведём единообразно с помощью диагонального процесса Г. Кантора.

Каждое действительное число х Î R можно записать в виде десятичной дроби х = ±А,a₁a₂ …a_n … , где ± Î {+, –}, А Î N È {0} – целая часть, а a₁ , a₂ , … , a_n , … – цифры от 0 до 9. Это представление неоднозначно: например, 1/2 = 0,50000… = 0,49999… ( в одном варианте записи, начиная со второй цифры после запятой, идут одни нули, а в другой – одни девятки). Чтобы запись была однозначной, мы будем выбирать первый вариант, т.е. не использовать десятичные представления с бесконечными “хвостами” из девяток. Тогда каждому числу будет соответствовать ровно одна десятичная запись.

Предположим, вопреки доказываемому, что удалось пересчитать все действительные числа. Тогда их можно расположить по порядку:

х₁ = ±А,x₁₁x₁₂x₁₃x₁₄ …

х₂ = ±В, x₂₁x₂₂x₂₃x₂₄ …

х₃ = ±С, x₃₁x₃₂x₃₃x₃₄ …

х₄ = ±D, x₄₁x₄₂x₄₃x₄₄ …

…………………..

В случае множества [0; 1] здесь будут только неотрицательные числа, у которых все целые части нулевые: А = В = С = D = … = 0.

Чтобы придти к противоречию, построим действительное число у Î [0; 1], которое не содержится в построенном списке. Именно, положим y = 0, y₁y₂ … , где y_i = .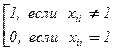

Например, если

x₁ = 2, 13453 …

х₂ = –3,40154 …

х₃ = 10,51961 …

х₄ = –13,67812 …

х₅ = 0,500013 …

………………… ,

то у = 0, 01101 … .

Построенное действительное число y не совпадает ни с одним из выписанных чисел, ведь оно отличается от каждого х_k по крайней мере k-ой цифрой десятичного разложения, а разным записям соответствуют различные числа.

Значит, предположив, что можно пересчитать все числа из R или из [0; 1], мы пришли к противоречию, указав число, которое “не сосчитано”. Следовательно, множества R и [0; 1] несчётны.

Теорема доказана.

Таким образом, множества R и N не являются эквивалентными, и N ÌR, поэтому всех действительных чисел действительно “больше”, чем натуральных. Говорят, что мощность множества R – мощность континуума, обозначаемая через c,больше, чем мощность N, обозначаемая через À₀: |N| = À₀ < < c = |R|. В то же время, как было доказано выше, |Z| = |Q| = |N| =À₀.