Функции специального вида
В математике важную роль играют функции, обладающие некоторыми специальными свойствами. Пусть f: A ® B – функция из А в B. Говорят, что f
| отображение, если | D(f) = A, т.е. " a Î A $ b Î B b = f(a) |
| сюръективна (наложение), если | Im(f) = B, т.е. " b Î B $ a Î A b = f(a) |
| инъективна (вложение), если | " b Î B $ ! a Î A b = f(a) или " a1 , a2 Î A f(a1) = f(a2) ® a1 = a2 |
| биективна, если | f – инъективное и сюръективное отображение |
Легко понять, что означают эти свойства на языке графов и графиков:
| Свойство | Граф | График |
| отображение | из каждой вершины · а Î А графа выходит одна стрелка:
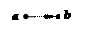
|  каждая вертикальная прямая x = a Î А пересекает график в одной точке
каждая вертикальная прямая x = a Î А пересекает график в одной точке
|
| сюръективность | в каждую вершину · b Î B графа входит хотя бы одна стрелка:
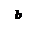 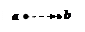
| 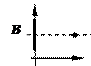 каждая горизонтальная прямая y = b Î B пересекает график хотя бы в одной точке
каждая горизонтальная прямая y = b Î B пересекает график хотя бы в одной точке
|
| инъективность | в каждую вершину · b Î B графа входит не более одной стрелки:

|  каждая горизонтальная прямая y = b Î B пересекает график ровно в одной точке
каждая горизонтальная прямая y = b Î B пересекает график ровно в одной точке
|
| биективность | все три предыдущие свойства | все три предыдущие свойства |
Примеры: 1. Пусть А ¹ Æ. Тогда функция idA : A ® A, заданная правилом " a Î A idA(a) = a,будет биективна.
 Действительно, чтобы в этом убедиться, проще всего построить график – он представляет собой диагональ D = {(a; a) Î A´A} и удовлетворяет всем требованиям биективности функции.
Действительно, чтобы в этом убедиться, проще всего построить график – он представляет собой диагональ D = {(a; a) Î A´A} и удовлетворяет всем требованиям биективности функции.
2. Функция f: R ® R, заданная правилом f(x) = ex, инъективна, но не сюръективна, а потому и не биективна, т.к. Im(f) = R+ ¹ R.
3. В отличие от предыдущего примера, функция f: R ® R+ , заданная правилом f(x) = ex, инъективна, сюръективна и биективна.
4. Функция f: R ® R, заданная правилом f(x) = sin x, не является ни инъективной, ни сюръективной, ни биективной.
5. Функция f: R ® R, заданная правилом f(x) = ln x, является инъективной и сюръективной, но не биективной, т.к. D(f) = R+ ¹ R, т.е. она – не является отображением.
Упражнение. Определите виды функций:
а) f : [0; 1] ® [0; 1], f(x) = ex, б) f : R ® [0; 1], f(x) = ex,
в)f : R ® R, f(x) = etg x, г)f : R ® R+, f(x) = etg x,
д) f : R ® R+, f(x) = ln(1 – x), е) f : [–1; 1] ® R , f(x) = ln(1 – x).
Дата добавления: 2021-12-14; просмотров: 603;











