Разрешимость аксиоматических теорий

Проблема разрешимости теории может быть сформулирована несколькими способами:

(Проблема доказуемости):Существует ли алгоритм, позволяющий за конечное число шагов эффективно определить, является ли заданная замкнутая формула теории доказуемой, или нет.

(Проблема общезначимости):Существует ли алгоритм, позволяющий за конечное число шагов эффективно определить, является ли заданная замкнутая формула теории общезначимой (т.е. тождественно истинной), или нет.

(Проблема выполнимости):Существует ли алгоритм, позволяющий за конечное число шагов эффективно определить, является ли заданная замкнутая формула теории выполнимой (т.е. не тождественно истинной и не тождественно ложной), или нет.

В этих формулировках участвует понятие алгоритма, которое строго определяется в курсе “Теория алгоритмов”, а пока будем воспринимать его на интуитивном уровне, считая, что алгоритм – это программа, написанная на некотором языке программирования и выполняемая на какой-то ЭВМ. Конечно, все формулы теории и её правила вывода предполагаются эффективно занумерованными натуральными числами, кроме того, естественно потребовать существования алгоритма, определяющего по заданному номеру формулы, является эта формула аксиомой теории или нет. Тогда будет существовать алгоритм, перечисляющий все доказуемые формулы теории (?!).

Теорема (об эквивалентности проблем доказуемости, общезначимости и выполнимости).Три сформулированные проблемы эквивалентны, т.е. существование алгоритма, решающего одну из них влечёт существование алгоритма, решающего остальные проблемы.

Доказательство. Предположим, что нашёлся алгоритм А(Ф), решающий проблему доказуемости т.е. программа, выдающая за конечное время по заданной замкнутой формуле теории Ф, ответ 1, если эта формула доказуема, и 0 – в противном случае. Этот же алгоритм решает и проблему общезначимости: нужно лишь вспомнить, что специальная теория полна в широком смысле, т.е. её формула тождественно истинна тогда и только тогда, когда она доказуема.

Если нашёлся алгоритм А(Ф), решающий проблему общезначимости, то для проверки выполнимости замкнутой формулы Ф применим его дважды: для Ф и для 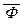. Ясно, что формула Ф выполнима тогда и только тогда, когда А(Ф) = = 0 = А( ).

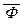Наконец, если нашёлся алгоритм А(Ф), решающий проблему выполнимости произвольной замкнутой формулы Ф, то для решения вопроса о доказуемости этой формулы(т.е. о её общезначимости) запустим этот алгоритм для формулы Ф. Если А(Ф) = 1, то формула Ф выполнима и не общезначима. Если же А(Ф) = 0, то Ф либо общезначима, либо тождественно ложна, т.е. является отрицанием общезначимой формулы. Теперь одновременно запустим алгоритмы перечисления доказуемых формул и их отрицаний (?!). Формула Ф обязательно встретится в одном из списков и её вид будет определён.

Теорема доказана.

Формальная теория называется разрешимой, если для неё существует алгоритм, решающий любую из трёх сформулированных эквивалентных проблем. Долгое время математики искали способы доказательства разрешимости основных математических теорий. В некоторых простейших случаях такие алгоритмы найти легко.

Теорема (о разрешимости исчисления высказываний).Формальная теория исчисления высказываний разрешима.

Доказательство. Это следует из возможности эффективной проверки общезначимости формулы путём построения таблицы истинности. Теорема доказана.

Основная трудность в определении общезначимости замкнутой формулы обусловлена наличием кванторов: как проверить истинность или ложность высказываний " x Î M P(x) или $ x Î M P(x), если множество M бесконечно, а P(x) – предикат на M ? Простой перебор значений объектной переменной x невозможен, т.к. может потребовать бесконечного времени. Таким образом, трудности возникают уже при проверке общезначимости простейших формул вида " x P(x) или $ x P(x). Проблемы с кванторами исчезают, если рассматривать

интерпретации формул на конечных множествах.

Теорема (об элиминации кванторов на конечном множестве).Если множество M = {m₁ , … , m_k} – конечно, то для любой формулы исчисления предикатов Ф(x) верно

(" x Î M Ф(x)) º (Ф(m₁) Ù … Ù Ф(m_k)), ($ x Î M Ф(x)) º (Ф(m₁) Ú … Ú Ф(m_k)).

Отсюда следует, что любая формула на конечном множестве равносильна некоторой бескванторной формуле.

Доказательство. Утверждения (" x Î M Ф(x)) º Ф(m₁) Ù … Ù Ф(m_k), ($ x Î M Ф(x)) º Ф(m₁) Ú … Ú Ф(m_k) верны по определению истинности высказываний с кванторами. Если дана произвольная формула F(x₁ , … , x_n), то можно считать, что она является ППНФ, т.е. имеет вид

F(x₁ , … , x_n) = (Q₁ y₁ Î M (Q ₂ y₂ Î M (…(Q _s y_s Î M G(x₁ , … , x_n , y₁ , … , y_s ))…))).

Теперь с помощью доказанных утверждений можно последовательно снимать квантор за квантором, получив в итоге бескванторную формулу.

Например, для формулы (" y Î M ($ z Î M G(x, y, z))) имеем:

(" y Î M ($ z Î M G(x, y, z))) º (" y Î M (G(x, y, m₁) Ú … Ú G(x, y, m_k))) º

º (G(x, m₁ , m₁) Ú … Ú G(x, m₁, m_k)) Ù … Ù (G(x, m_k , m₁) Ú … Ú G(x, m_k , m_k)).

Теорема доказана.

Следствие (об n-разрешимости).Пусть n – фиксированное натуральное число. Для любой формулы исчисления предикатов существует алгоритм, выясняющий за конечное число шагов, принимает ли она значение 0 хотя бы при одной интерпретации на n-элементном множестве, или же при всех интерпретациях на n-элементных множествах эта формула принимает значение 1.

Доказательство.Для n-элементного множества M = {a₁ , … , a_n } существует лишь конечное число интерпретаций заданной формулы Ф : это следует из конечности числа предикатов на множестве M. Последовательно перечисляя эти интерпретации и вычисляя значение формулы при каждой из них, либо найдём интерпретацию со значением 0, либо получим, что при всех интерпретациях значение формулы равно 1. Следствие доказано.

Возникает идея доказать следующее

“Утверждение” (об опровержении формул на конечных множествах). Если формула исчисления предикатов не является тождественно истинной, то существует её интерпретация на конечном множестве, при которой эта формула принимает значение 0.

Отсюда уже почти был бы виден алгоритм проверки заданной замкнутой формулы исчисления предикатов на общезначимость. Просто нужно последовательно вычислять значения формулы при её интерпретациях сначала на одноэлементных множествах, затем на двухэлементных, и.т.д. Если она не общезначима, то на некотором конечном шаге обязательно получится значение ложь. Правда, этот алгоритм может работать бесконечно, если формула общезначима. Но, кажется, – ещё чуть-чуть – и проблема будет решена… Однако, надеждам на доказательство сформулированного выше утверждения не суждено сбыться:

Утверждение (о выполнимой формуле, истинной на всех конечных моделях).Формула исчисления предикатов

($ x (" y ($ z ((P(y, z) ® P(x, z)) ® (P(x, x) ® P(y, x))))))

истинна на любой конечной модели, но не тождественно истинна.

Доказательство. Прежде всего, эта формула принимает значение ложь при интерпретации (N, £ ):

($ x Î N (" y Î N ($ z Î N ((y £ z) ® (x £ z)) ® ((x £ x) ® (y £ x)))))) º

º ($ x Î N (" y Î N ($ z Î N ((y £ z) ® (x £ z)) ® ( 1 ® (y £ x)))))) º

º ($ x Î N (" y Î N ($ z Î N ((y > z) Ú (x £ z)) ® (y £ x))))) º

º ($ x Î N (" y Î N ($ z Î N ((y £ z) Ù (x > z)) Ú (y £ x)))))

и условие (y £ x) не может быть истинным при y > x , т.е. при y > x должно выполняться ((y £ z) Ù (x > z)), что невозможно (если z < x и y £ z, то y < x).

Докажем теперь, что в случае ложности формулы на модели (M, P(_ , _) ) множество М бесконечно. В самом деле, ложность этой формулы означает

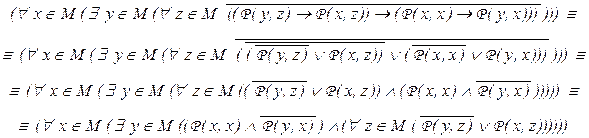
Таким образом, для любого x Î M существует y = y(x) Î M со свойствами: Р(х, х) = 1, Р(y(x), x) = 0 и для любого z верно Р(y(x), z) = 0 или Р(x, z) = 1.

Рассмотрим последовательность элементов множества М: x₁ = x, x_i+1 = y(x_i) (i Î N ) и докажем, что среди её элементов нет равных. В самом деле, если x_i = x_j при i < j, то x_j = y(x_j–1) и Р(x_j , x_j–1 ) = Р(y(x_j–1), x_j–1 )= 0, но (при x = x_i , z = x_j–1) Р(x_i+1 , x_j–1 ) = 0 или Р(x_i , x_j–1 ) = 1. Случай Р(x_i , x_j–1 ) = 1 противоречит условиям x_i = x_j и Р(x_j , x_j–1 ) = 0. Значит, Р(x_i+1 , x_j–1 ) = 0, и аналогично предыдущему при x = x_i+1 , z = x_j–1 получаем Р(x_i+2 , x_j–1 ) = 0 или Р(x_i+1 , x_j–1 ) = 1. Отсюда Р(x_i+2 , x_j–1 ) = 0 , и процесс можно продолжить, пока не получим Р(x_j–2 , x_j–1 ) = 0, что ведёт к противоречию: при x = x_j–2 , z = x_j–1 имеем Р(x_j–1 , x_j–1 ) = 0 или Р(x_j–2 , x_j–1 ) = 1 (альтернатива Р(x_j–1 , x_j–1 ) = 0 невозможна ввиду Р(х, х) = 1).

Утверждение доказано.

Таким образом, наша первая попытка построить алгоритм разрешения формальной теории предикатов успешно провалилась ! В 20-х годах прошлого века было исследовано много и значительно более тонких идей построения алгоритма проверки доказуемости формул исчисления предикатов. Все они не привели к желаемому результату. Каково же было удивление математиков, когда в 30-х годах XX в. А. Чёрчем было доказано, что не существует алгоритма проверки заданной формулы исчисления предикатов на общезначимость.

Теорема (Чёрча о неразрешимости теории исчисления предикатов). Не существует алгоритма, позволяющего за конечное число шагов определить, является ли заданная формула исчисления предикатов общезначимой, или нет.

Тем не менее, для некоторых формул специального вида алгоритмы, решающие проблемы общезначимости и выполнимости существуют. Приведём для примера два результата о замкнутых формулах с одноимёнными кванторами.

Теорема (об общезначимых замкнутых $-формулах).Замкнутая ППНФ, содержащая только кванторы существования, является общезначимой тогда и только тогда, когда она принимает значение 1 – истина во всех интерпретациях на одноэлементных множествах.

Доказательство.Рассмотрим замкнутую ППНФ, содержащую только кванторы существования, т.е. формулу вида ($ x ($ y (… ($ z F(x, y, … , z))…))), не зависящую от других переменных, кроме связанных кванторами. Ясно, что если она общезначима, то во всех интерпретациях на одноэлементных множествах она принимает значение истина.

Обратно, если эта формула не общезначима, то она принимает значение ложь при интерпретации на некотором множестве M. Тогда отрицание этой формулы, т.е. формула (" x (" y (… (" z 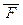(x, y, … , z)) …))),будет при этой интерпретации иметь значение истина. В частности, зафиксировав m₀ Î M, получим 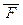(m₀ , m₀ , … , m₀ ) = 1. Таким образом, F(m₀ , m₀ , … , m₀ ) = 0 и значит, формула ($ x ($ y (… ($ z F(x, y, … , z))…))) принимает значение ложь при интерпретации на одноэлементном множестве {m₀ }.

Теорема доказана.

Теорема (об общезначимых замкнутых "-формулах).Замкнутая ППНФ, содержащая только n кванторов всеобщности, является общезначимой тогда и только тогда, когда она принимает значение 1 во всех интерпретациях на n-эле­ментных множествах.

Доказательство. Рассмотрим замкнутую ППНФ, содержащую только n кванторов всеобщности, т.е. формулу вида (" x (" y (… (" z F(x, y, … , z))…))), не зависящую от других переменных, кроме связанных кванторами.

Ясно, что если она общезначима, то во всех интерпретациях на n-элементных множествах она принимает значение истина.

Обратно, если эта формула не общезначима, то она принимает значение ложь при интерпретации на некотором множестве M. Тогда отрицание этой формулы, т.е. формула ($ x ($ y (… ($ z 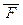(x, y, … , z))…))),будет при этой интерпретации иметь значение истина. Таким образом, 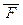(m₁ , m₂ , … , m_n ) = 1 при некоторых m₁ , … , m_n Î M. Поэтому F(m₁ , … , m_n ) = 0 и исследуемая формула (" x (" y (… (" z F(x, y, … , z))…))) принимает значение ложь при интерпретации на множестве {m₁ , … , m_n }.

Теорема доказана.

Что касается формальной теории арифметики, то после всего сказанного неудивительно, что она тоже неразрешима:

Теорема (Чёрча о неразрешимости формальной арифметики). Не существует алгоритма, позволяющего за конечное число шагов определить, является ли заданная формула формальной арифметики доказуемой, или нет.

Более того, в 70-х годах XX в. было доказано, что алгоритмически неразрешим вопрос о существовании целочисленных решений диофантовых уравнений, т.е. уравнений вида F(x₁ , … , x_n ) = 0, где F(x₁ , … , x_n ) – ненулевой многочлен от переменных x₁ , … , x_n с целыми коэффициентами. Таким образом, не существует алгоритма проверки доказуемости формул формальной арифметики вида ($ x₁ ($ x₂ ( … ($ x_n (F(x₁ , … , x_n ) = 0))))). Можно даже конкретно указать многочлен F(x₁ , … , x_n ). Это утверждение, доказанное в 1970 г. Ю.В. Матиясевичем, решает 10-ю проблему Гильберта из списка поставленных им в 1901 г. на Международном математическом конгрессе в Париже наиболее важных математических задач XX века.