Неразрешимость проблемы Гильберта

Мы теперь вплотную подходим к той цели, ради которой Тьюринг с самого начала разрабатывал свою теорию — получить ответ на вопрос, заключенный в общей проблеме алгоритмической разрешимости, поставлен­ной Гильбертом, а именно: существует ли некая механическая процедура для решения всех математических задач, принадлежащих к некоторому широкому, но вполне опре­деленному классу? Тьюринг обнаружил, что он мог бы перефразировать этот вопрос сле­дующим образом: остановится ли в дей­ствительности n-я машина Тьюринга, если на ее вход поступит число т? Эта зада­ча получила название проблемы остановки. Не так сложно составить список команд, для которых машина никогда не остановит­ся при любом т (как, например, в случаях п = 1 или 2, рассмотренных в предыду­щем разделе, а также во всех случаях, когда вообще отсутствует команда STOP). Точно так же существует множество списков ко­манд, для которых машина будет остана­вливаться всегда, независимо от вводимого числа m (например, Гц). Кроме того, неко­торые машины при работе с одними числами останавливались бы, а с другими — нет. Со­вершенно очевидно, что алгоритм, который никогда не прекращает работу, бесполезен. Это, собственно, и не алгоритм вовсе. По­этому важно уметь ответить на вопрос, при­ведет ли когда-нибудь работа машины Т_п над данным числом m к какому-то ответу или нет! Если нет (т. е. процесс вычисле­ния никогда не прекращается), то я буду выражать это следующей записью:

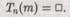
(Сюда же включены машины, которые в хо­де работы попадают в ситуацию, когда нет команды, определяющей их дальнейшее по­ведение, как это было в случае рассмотрен­ных выше фиктивных машин Тл, и Т?. К со­жалению, наша на первый взгляд работо­способная машина уз должна теперь также считаться фиктивной, т.е. Тз(ггс) = D, по­скольку результатом ее действия всегда будет просто пустая лента, тогда как нам, чтобы приписать номер полученному ответу, нуж­на хотя бы одна единица на выходе! Маши­на Г| |, однако, совершенно полноправна, поскольку она производит единственную 1. Результатом ее работы будет лента с номе­ром 0, так что Т₁₁ (m) = 0 для любого m.)

В математике весьма важно иметь воз­можность установить момент, когда маши­на Тьюринга остановится. Рассмотрим для примера уравнение

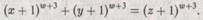
(Не пугайтесь, даже если Вы не любите вни­кать в детали математических вычислений. Это уравнение используется здесь только в качестве примера, и от вас не требуется его глубокого понимания.) Это конкретное уравнение относится к известной (возмож­но, самой известной) и пока нерешенной математической проблеме. Проблема фор­мулируется следующим образом: существу­ет ли какой-либо набор х, у, z, w, для ко­торого это равенство выполняется. Знаме­нитое утверждение, записанное на полях «Арифметики» Диофанта великим француз­ским математиком семнадцатого столетия Пьером де Ферма (1601-1665) и известное как «последняя теорема Ферма», гласит, что это равенство никогда не выполняется). Будучи адвокатом по профессии, Ферма тем не менее был искуснейшим математиком своего времени. (Ферма был современником Декарта.) В своей записи он утверждал, что знает «воистину прекрасное доказательство» своей теоремы, но поля книги слишком ма­лы, чтобы его привести. До сегодняшнего дня никому так и не удалось ни воспроиз­вести это доказательство, ни найти опро­вергающий это утверждение пример!

Очевидно, что для заданной четверки чисел (х, у, z, w) выяснить, выполняется это равенство или нет, можно простым вычисле­нием. Значит, мы можем представить себе вычислительный алгоритм, который после­довательно перебирает все возможные че­тверки чисел одну за другой и останавлива­ется только тогда, когда равенство удовле­творяется. (Мы уже знаем, что для конечных наборов чисел существуют способы их ко­дирования на ленте вычислимым способом, а именно, в виде одного числа. Таким обра­зом, перебор всех четверок можно провести, просто следуя естественному порядку соот­ветствующих им одиночных чисел.) Если бы мы могли установить, что этот алгоритм ни­когда не останавливается, то это стало бы доказательством утверждения Ферма.

Сходным образом в терминах проблемы остановки машины Тьюринга можно пере­фразировать многие другие нерешенные ма­тематические проблемы. Примером такого рода проблем может служить так называе­мое предположение Гольдбаха: любое четное число, большее двух, может быть предста­влено в виде суммы двух простых чисел⁶). Процесс, с помощью которого можно уста­новить, относится некоторое натуральное число к простым или нет, является алго­ритмическим, поскольку достаточно прове­рить делимость данного числа на все числа, меньшие его, а это достигается с помощью конечного числа вычислительных операций. Мы можем придумать машину Тьюринга, которая перебирает четные числа 6, 8, 10, 12, 14, ... , пробуя все возможные способы разбиения их на пары нечетных чисел

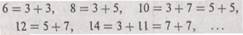
и убеждаясь, что для каждого четного чи­сла какое-то из разбиений образовано двумя простыми числами. (Очевидно, нам не на­до проверять пары четных слагаемых, кроме 2 + 2, поскольку все простые числа за ис­ключением 2 — нечетные.) Наша машина должна остановиться только в том случае, если она находит четное число, для которого ни одно из разбиений не является парой про­стых чисел. В этом случае мы получили бы контрпример к предположению Гольдбаха, т. е. нашли бы четное число, большее 2, которое не является суммой двух простых чисел. Следовательно, если бы мы могли установить, останавливается машина Тью­ринга когда-нибудь или нет, то тем самым мы выяснили бы, справедливо предположе­ние Гольдбаха или нет.

Возникает естественный вопрос: каким образом следует определять, остановится какая-то определенная машина Тьюринга (в которую введены конкретные начальные данные) или нет? Для многих машин Тью­ринга ответить на этот вопрос нетрудно, но, как мы видели выше, иногда для ответа мо­жет потребоваться решение какой-нибудь до сих пор не решенной математической задачи. Так существует ли некая алгоритми­ческая процедура для решения общей про­блемы — проблемы остановки — полностью механическим путем? Тьюринг показал, что такой процедуры на самом деле нет.

В сущности, его доказательство своди­лось к следующему. Предположим, наобо­рот, что указанный алгоритм существует. Тогда существует и некая машина Тьюринга Н, которая «решает», остановится ли в кон­це концов n-я машина Тьюринга, действуя на число т. Условимся, что результатом действия машины Н будет лента с номе­ром 0, если n-я машина не останавливается, и с номером 1 в противоположном случае:

Здесь мы могли бы воспользоваться спосо­бом кодирования пары (п, т), использован­ным ранее для универсальной машины Тью­ринга U. Однако это привело бы к пробле­ме технического характера, поскольку при некоторых п (например, п = 7) Т_n будет определена некорректно, и маркер 111101будет непригоден для отделения на ленте п от т. Чтобы избежать этой проблемы, бу­дем полагать, что п представлено не в дво­ичной, а в расширенной двоичной форме, тогда как для m будет по-прежнему исполь­зоваться обычная двоичная запись. В этом случае комбинации 110будет достаточно для разделения пит. Использование точки с запятой в обозначении Н(п; т) в отличие от запятой в обозначении универсальной машины U(n, т) указывает на это различие в кодировании.

Представим себе теперь бесконечную таблицу, в которую включены окончатель­ные результаты действий всех возможных машин Тьюринга на все возможные (раз­личные) входные данные. В этой табли­це N-Й ряд представляет собой результаты вычислений n-й машины Тьюринга, по­лученные при ее работе последовательно с т = 0, 1, 2, 3, 4, ... :

Я немного «сжульничал» и не стал рас­полагать машины Тьюринга по порядку их действительных номеров. Если бы я так сде­лал, то получился бы список, начало которого выглядело бы слишком скучным, по­скольку все машины при значениях п мень­ших 11 не дают ничего, кроме D, а для п = 11 мы имеем просто нули. Дабы сде­лать начало этой таблицы более интерес­ным, я предположил, что мы использовали некую гораздо более эффективную систему кодирования. Фактически, я просто при­своил ячейкам более или менее произволь­ные значения, только чтобы дать вам общее представление о том, как может выглядеть эта таблица.

На самом деле нам не требуется, чтобы эта таблица была построена путем вычисле­ний, скажем, с помощью некоторого алго­ритма. (На самом деле, как мы увидим далее, такого алгоритма и не существует.) Доста­точно просто представить себе, что каким-то образом истинный список попал в наше распоряжение, возможно, с помощью Бога! Если бы мы попытались получить эту табли­цу с помощью вычислений, то именно сим­волы П вызвали бы затруднения, поскольку мы не могли бы с уверенностью сказать, когда в той или иной ячейке должен быть помещен символ П — ведь соответствующие вычисления никогда не заканчиваются!

Тем не менее искомую таблицу мож­но построить с помощью вычислительной процедуры, если использовать нашу гипо­тетическую машину Н, поскольку она мог­ла бы определить, где на самом деле по­являются значения D. Однако вместо этого мы используем машину Я для того, чтобы избавиться от появления значений П в та­блице, заменив их во всех случаях нулями. Это достигается за счет вычисления значе­ния Н(п;т), предваряющего действие Т_n на т, после чего мы позволим Т_n произво­дить соответствующие действия, только если Н(п; т) = 1 (т. е. только тогда, когда вы­числение Т_n(т) приводит к определенному результату), и будем просто записывать в со­ответствующую ячейку 0 при Н(п; т) = 0 (т. е. если Т_n(т) = ). Мы можем запи­сать эту новую процедуру, представляющую собой последовательное действие Н(п; т) и Т_n(т), как

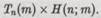
(Здесь я использую общепринятую в мате­матике договоренность о последовательно­сти выполнения действий, согласно которой операция, записанная справа, должна вы­полняться первой. Обратите внимание, что в этом случае можно символически записать  х 0 = 0.)

Теперь таблица принимает следующий вид:

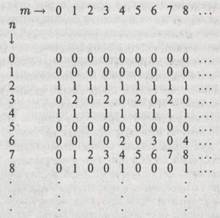
Заметьте, что, исходя из предположения су­ществования машины Н, мы получаем ряды таблицы, состоящие из вычислимых после­довательностей. (Под «вычислимой после­довательностью» я понимаю бесконечную последовательность, элементы могут быть найдены один за другим посредством неко­его алгоритма; это означает, что существует некоторая машина Тьюринга, которая, бу­дучи применена поочередно к натуральным числам т = 0, 1, 2, 3, 4, 5, ... , произво­дит члены рассматриваемой последователь­ности.) Обратите внимание на следующие два факта относительно этой таблицы. Во-первых, любая вычислимая последователь­ность натуральных чисел должна появиться где-то (может быть, далеко не сразу) среди рядов таблицы. Это свойство выполнялось уже и для исходной таблицы, содержавшей значения . Мы просто добавили несколько рядов, чтобы заменить «фиктивные» маши­ны Тьюринга (т. е. такие, которые приводят к  хотя бы в одном случае). Во-вторых, считая, что машина Тьюринга Н существу­ет, мы получили таблицу вычислительным путем (т. е. с помощью некоторого опреде­ленного алгоритма), а именно, посредством процедуры Т_п(т) х Н(п; т). Иными слова­ми, существует некая машина Тьюринга Q, применение которой к паре чисел (n, т) дает значение соответствующей ячейки та­блицы. Для этой машины числа пит на ленте можно кодировать таким же обра­зом, как и для Н, т. е. мы имеем

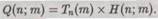
Воспользуемся теперь разновидностью остроумного и мощного приема, так назы­ваемого диагонального процесса Георга Кан­тора. (Мы познакомимся с оригинальным вариантом этого метода в следующей главе.) Рассмотрим значения в ячейках, располо­женных на главной диагонали таблицы — диагональные элементы (матрицы), — вы­деленные жирнымшрифтом:

Эти элементы образуют некоторую последо­вательность 0, 0, 1, 2, 1, 0, 3, 7, 1,... , к каж­дому члену которой мы теперь прибавим единицу:

Это, безусловно, механическая процедура, и, поскольку наша таблица была получена путем вычислений, мы получим новую вы­числимую последовательность 1 + Q(n,n ), т.е.

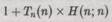
(с учетом того, что для диагональных эле­ментов п = m). Но наша таблица содержит в себе все вычислимые последовательности, поэтому она должна содержать также и но­вую последовательность. Однако это невоз­можно! Ведь наша новая последовательность отличается от первого ряда первым элемен­том, от второго — вторым, от третьего -третьим, и т.д. Налицо явное противоречие, которое и устанавливает справедливость до­казываемого нами утверждения о том, что машина Тьюринга Н на самом деле не суще­ствует! Иными словами, не существует уни­версального алгоритма для решения вопроса об остановке произвольной машины Тьюринга. Можно построить доказательство и по-другому. Для этого заметим, что из предпо­ложения о существовании Н следует и суще­ствование машины Тьюринга с номером k, реализующей алгоритм (диагональный про­цесс!) 1 + Q(n; п), т. е. можно записать

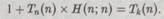
Но если мы подставим в это выражение п = k, то получится

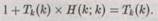
Мы приходим к противоречию, потому что если Т_k(k) останавливается, то мы имеем невыполнимое равенство

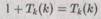
(поскольку H(k;k) = 1), тогда как в слу­чае безостановочного действия T_k(k) (т.е. когда H(k, k) = 0) мы получаем не менее абсурдное соотношение

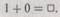
Вопрос о том, останавливается ли кон­кретная машина Тьюринга или нет, предста­вляет собой совершенно четко определен­ную математическую задачу (а ранее мы уже видели, что, наоборот, различные важные математические задачи могут быть сведены к вопросу об остановке машины Тьюринга). Таким образом, доказав, что не существует алгоритма для решения вопроса об останов­ке машины, Тьюринг показал (также как и Черч, который использовал свой собствен­ный и весьма отличающийся подход), что не может быть и общего алгоритма для ре­шения математических задач. Проблема раз­решимости Гильберта не имеет решения!

Это не означает, что в каждом отдель­ном случае мы не в состоянии выяснить справедливость (или, наоборот, несостоя­тельность) некоторого конкретного мате­матического утверждения или определить, остановится ли данная машина Тьюрин­га. С помощью интуиции, искусных тех­нических приемов или же опираясь просто на здравый смысл, мы, вероятно, могли бы получить ответ на такие вопросы в част­ных случаях. (Так, например, если перечень инструкций некоторой машины Тьюринга не включает ни одной команды STOP или же, наоборот, состоит только из таких ко­манд, то одного здравого смысла достаточ­но для решения вопроса о ее остановке!) Но не существует ни одного алгоритма, ко­торый позволял бы решать любую матема­тическую задачу или давал ответ на вопрос об остановке любой машины Тьюринга при любых вводимых в нее числах.

Может показаться, что мы пришли к выводу о существовании no-крайней ме­ре нескольких неразрешимых математичес­ких вопросов. Однако это совсем не так! Мы не показали, что существует какая-то необычайно громоздкая машина Тьюрин­га, для которой (в некотором абсолютном смысле) невозможно решить вопрос об оста­новке при ее работе с каким-то особенно громоздким числом — в действительности, все как раз наоборот, как мы сможем скоро убедиться. Мы вообще ничего не говорили о неразрешимости какой-то отдельной зада­чи, а только лишь об алгоритмической не­разрешимости классов задач. В каждом кон­кретном случае ответ будет либо «да», либо «нет», поэтому алгоритм для решения част­ной задачи, конечно, существует, а именно алгоритм, который при применении к этой задаче просто дает ответ «да» или, может быть, «нет»! Трудность в данном случае со­стоит в том, что мы не знаем, какой именно из имеющихся алгоритмов применять в том или ином случае. Это вопрос об установле­нии математической истинности отдельно­го утверждения, но не об общем решении проблемы для целого класса утверждений. Очень важно сознавать, что сами по себе алгоритмы не доказывают математическую истину. Решение о правомерности исполь­зования каждого алгоритма должно всегда приходить извне.