Независимость системы аксиом теории
Создавая аксиоматическую теорию, естественно стремиться не выписывать лишних аксиом – тех, которые выводимы из остальных. Система аксиом формальной теории называется независимой, если ни одна аксиома этой системы не выводима из остальных. Более формально, ситема {Ai}i Î I независима, если для любой аксиомы Аi и любого конечного множества аксиом Г Í {Aj}j Î I \ {i} утверждение Г  Аi неверно.
Аi неверно.
Конечно, требование независимости является скорее эстетическим, нежели математически необходимым, но оно побуждает к анализу взаимосвязей аксиом создаваемой теории, к отсечению лишнего, тем самым, – к более глубокому пониманию сути математической реальности. Вот почему независимость системы аксиом является “правилом хорошего тона” для создателя аксиоматики.
Если аксиоматика формальной теории состоит из схем аксиом, то, как правило, проверяют независимость друг от друга схем аксиом, а не отдельных аксиом теории.
Как доказать независимость той или иной системы аксиом ? Основным методом доказательства является метод построения независимых моделей, основанный на следующей теореме:
Теорема (критерий независимости системы аксиом).Система аксиом (схем аксиом) {Ai}i Î I независима тогда и только тогда, когда для каждого i Î I существует модель для системы аксиом (схем аксиом) {Aj}j Î I \ {i} , в которой аксиома (схема аксиом) Аi ложна.
Доказательство. Ясно, что существование модели с указанным в формулировке теоремы свойством показывает, что утверждение Г  Аi для любого конечного множества аксиом Г Í {Aj}j Î I \ {i} неверно.
Аi для любого конечного множества аксиом Г Í {Aj}j Î I \ {i} неверно.
Обратно, если аксиома Аi не выводима из остальных, то непротиворечивой будет система аксиом Гi = {Aj}j Î I \ {i} È { 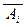 } . Действительно, если бы эта система была противоречива, то любая формула была бы доказуема (выводима из некоторой конечной совокупности аксиом Г È {
} . Действительно, если бы эта система была противоречива, то любая формула была бы доказуема (выводима из некоторой конечной совокупности аксиом Г È { 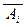 }, где Г Í Гi ).Поэтому Г,
}, где Г Í Гi ).Поэтому Г, 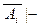 Ai и, очевидно, Г,
Ai и, очевидно, Г,  . По правилу опровержения отсюда следует, что Г
. По правилу опровержения отсюда следует, что Г 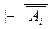 , т.е. (с учётом аксиомы
, т.е. (с учётом аксиомы 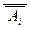 ® Ai ) верно Г
® Ai ) верно Г  Аi – противоречие. У непротиворечивого множества аксиом Гi = {Aj}j Î I \ {i} È {
Аi – противоречие. У непротиворечивого множества аксиом Гi = {Aj}j Î I \ {i} È { 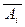 } существует модель, в которой аксиома Аi ложна, что и требовалось.
} существует модель, в которой аксиома Аi ложна, что и требовалось.
Теорема доказана.
Теорема (о независимости системы аксиом исчисления высказываний).Система аксиом формального исчисления высказываний (приведённая в § 1 главы III) независима.
Доказательство. Используем метод построения независимых моделей: для каждой схемы аксиом построим модель, в которой эта схема аксиом ложна, а остальные истинны. Все модели будут устроены однообразно: на некотором конечном множестве М определим функции из М в М : Ù , Ú , ® от двух аргументов и 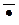 – от одного, которые будут интерпретировать логические связки исчисления высказываний. В каждом случае будет выделено некоторое подмножество И Í М, в котором находятся значения всех “истинных” в модели М схем аксиом, в отличие от независимой от них (“ложной” в М) схемы аксиом, которая принимает значения и не лежащие во множестве И. При этом применение правила modus ponens к формулам, имеющим значения только в И (к “истинным” в модели формулам), приводит снова к формуле, имеющем значения снова во множестве И (к “истинной” в модели формуле). Таким образом, все выводимые из “истинных” формул формулы снова будут истинными, а любая “ложная” формула не выводима из “истинных”. Итак, рассматриваемая в каждом случае “ложная” схема аксиом не выводится из остальных “истинных” аксиом.
– от одного, которые будут интерпретировать логические связки исчисления высказываний. В каждом случае будет выделено некоторое подмножество И Í М, в котором находятся значения всех “истинных” в модели М схем аксиом, в отличие от независимой от них (“ложной” в М) схемы аксиом, которая принимает значения и не лежащие во множестве И. При этом применение правила modus ponens к формулам, имеющим значения только в И (к “истинным” в модели формулам), приводит снова к формуле, имеющем значения снова во множестве И (к “истинной” в модели формуле). Таким образом, все выводимые из “истинных” формул формулы снова будут истинными, а любая “ложная” формула не выводима из “истинных”. Итак, рассматриваемая в каждом случае “ложная” схема аксиом не выводится из остальных “истинных” аксиом.
Все вычисления подробно производиться не будут (это – задание для самостоятельной работы), но конструкции моделей будут описаны точно.Посколькусвязка импликации участвует во всех аксиомах исчисления высказываний, доказательство независимости аксиом группы импликации наиболее трудоёмко.
Независимость схемы (И1): (А ® (B ® A)) .Рассмотрим трёхэлементное множество М = {0, 1, 2} и определим на нём новое исчисление логических связок, полагая для x, y Î M следующие значения связок: x Ù y = min{x, y}, x Ú y = = max{x, y}, x ® y = 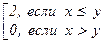 ,
, 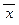 = 2 – x .
= 2 – x .
Проверим, что все схемы аксиом, кроме (И1) дают значения во множестве И = {2}, множество “истинных” формул замкнуто относительно правила modus ponens,а схема аксиом (И1) принимает значения не только во множестве И. Всё это проверяется путём построения многочисленных таблиц истинности.
| А | В | В ® A | А ® (B ® A) | А | В | А ® В | |
| 0 | 0 | 2 | 0 | 0 | 2 | ||
| 1 | 0 | 2 | 1 | 0 | 0 | ||
| 2 | 0 | 2 | 2 | 0 | 0 | ||
| 0 | 1 | 0 | 0 | 1 | 2 | ||
| 1 | 1 | 2 | 1 | 1 | 2 | ||
| 2 | 1 | 2 | 2 | 1 | 0 | ||
| 0 | 2 | 0 | 0 | 2 | 2 | ||
| 1 | 2 | 0 | 1 | 2 | 2 | ||
| 2 | 2 | 2 | 2 | 2 | 2 |
Таблица слева показывает, что схема аксиом (И1) не всегда принимает значения во множестве И = {2}, а потому “ложна в рассматриваемой модели”. Таблица справа доказывает, что множество “истинных” формул замкнуто относительно правила modus ponens (более точно, если А = 2 = (А ® B) , то B = 2).
Наконец, проверим, что все остальные схемы аксиом “истинны” в этой модели, т.е. принимают значения только во множестве И = {2}:
| А | В | С | А ® B | А ® C | B ® C | A ® (B ® C) | (A ® B) ® (А ® C) | (И2) | В Ù C | A ® (B Ù C) | (A ® С) ® (A ® (B Ù C)) | (К3) | А Ú В | (A Ú B) ® C | (B ® C) ® ((A Ú B) ® C) | (Д3) |
| 0 | 0 | 0 | 2 | 2 | 2 | 2 | 2 | 0 | 2 | 2 | 0 | 2 | 2 | |||
| 1 | 0 | 0 | 0 | 0 | 2 | 2 | 2 | 0 | 0 | 2 | 1 | 0 | 2 | |||
| 2 | 0 | 0 | 0 | 0 | 2 | 2 | 2 | 0 | 0 | 2 | 2 | 0 | 2 | |||
| 0 | 1 | 0 | 2 | 2 | 0 | 2 | 2 | 0 | 2 | 2 | 1 | 0 | 2 | |||
| 1 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 2 | |||
| 2 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 2 | 0 | 2 | |||
| 0 | 2 | 0 | 2 | 2 | 0 | 2 | 2 | 0 | 2 | 2 | 2 | 0 | 0 | |||
| 1 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 2 | |||
| 2 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 2 | |||
| 0 | 0 | 1 | 2 | 2 | 2 | 2 | 2 | 0 | 2 | 2 | 0 | 2 | 2 | |||
| 1 | 0 | 1 | 0 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 1 | 2 | 2 | |||
| 2 | 0 | 1 | 0 | 0 | 2 | 2 | 2 | 0 | 0 | 2 | 2 | 0 | 2 | |||
| 0 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 1 | 2 | 2 | |||
| 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 1 | 2 | 2 | |||
| 2 | 1 | 1 | 0 | 0 | 2 | 2 | 2 | 1 | 0 | 2 | 2 | 0 | 2 | |||
| 0 | 2 | 1 | 2 | 2 | 0 | 2 | 2 | 1 | 2 | 2 | 2 | 0 | 0 | |||
| 1 | 2 | 1 | 2 | 2 | 0 | 0 | 2 | 1 | 2 | 2 | 2 | 0 | 0 | |||
| 2 | 2 | 1 | 2 | 0 | 0 | 0 | 0 | 1 | 0 | 2 | 2 | 0 | 2 | |||
| 0 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 2 | 2 | 0 | 2 | 2 | |||
| 1 | 0 | 2 | 0 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 1 | 2 | 2 | |||
| 2 | 0 | 2 | 0 | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 2 | 2 | 2 | |||
| 0 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 1 | 2 | 2 | |||
| 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 1 | 2 | 2 | |||
| 2 | 1 | 2 | 0 | 2 | 2 | 2 | 2 | 1 | 0 | 0 | 2 | 2 | 2 | |||
| 0 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |||
| 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | |||
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
Таблица показывает, что схемы (И2), (К3), (Д3) “истинны” в этой модели.
| А | В | А Ù В | К1 | К2 | А Ú В | Д1 | Д2 | 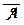
| 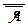
| О1 | О2 | A ® B | 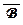 ® ® 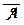
| О3 |
| 0 | 0 | 0 | 0 | 2 | 0 | 2 | 2 | |||||||
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |||||||
| 2 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | |||||||
| 0 | 1 | 0 | 1 | 2 | 0 | 2 | 2 | |||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | |||||||
| 2 | 1 | 1 | 2 | 0 | 2 | 0 | 0 | |||||||
| 0 | 2 | 0 | 2 | 2 | 0 | 2 | 2 | |||||||
| 1 | 2 | 1 | 2 | 1 | 1 | 2 | 2 | |||||||
| 2 | 2 | 2 | 2 | 0 | 2 | 2 | 2 |
Итак, схемы аксиом (К1), (К2), (Д1), (Д2), (О1), (О2), (О3) тоже “истинны” в построенной модели. Поэтому доказана независимость аксиомы (И1) от остальных аксиом формального исчисления высказываний.
Независимость схемы (И2): ((А ® (B ® С)) ® ((A ® B) ® (A ® C))) . Возьмём М = {0, 1, 2}, И = {0} и определим для x, y Î M следующие значения связок: x Ù y = max{x, y}, x Ú y = min{x, y}, x ® y = max{0, y – x}, 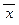 = 2 – x.
= 2 – x.
Проверьте самостоятельно, что все схемы аксиом, кроме (И2) принимают значения во множестве И, множество “истинных” формул замкнуто относительно правила modus ponens,а схема аксиом (И2) принимает значения не только во множестве И.
Независимость схемы (К1): ((A Ù B) ® A) . Возьмём М = {0, 1}, И = {1} и определим для элементов x, y Î M следующие значения логических связок: x Ù y = y, а остальные связки Ú , ® , 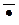 интерпретируем стандартно.
интерпретируем стандартно.
Следующие таблицы доказывают, что схема аксиом (К1) “ложна в рассматриваемой модели”, а множество “истинных” формул замкнуто относительно правила modus ponens (более точно, если А = 1 = (А ® B) , то B = 1):

Проверим теперь истинность остальных аксиом.
| А | В | А Ù В | К2 | А Ú В | Д1 | Д2 | 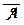
| 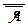
| О1 | О2 | А ® B | 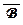 ® ® 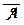
| О3 |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | ||||||
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | ||||||
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| А | В | С | А ® В | А ® C | B ® C | B ® А | И1 | A ® (B ® C) | (A ® B) ® (А ® C) | И2 | В Ù C | A ® (B Ù C) | (A ® С) ® (A ® (B Ù C)) | К3 | А Ú В | (A Ú B) ® C | (B ® C) ® ((A Ú B) ® C) | Д3 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | ||||
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | ||||
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | ||||
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | ||||
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | ||||
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Независимость схемы (К2): ((A Ù B) ® B) . Докажите самостоятельно, видоизменив интерпретацию конъюнкции.
Независимость схемы (К3): ((A ® B) ® ((A ® C) ® (A ® (B Ù C)))) . Возьмём М = {0, 1}, И = {1} и определим для элементов x, y Î M следующие значения логических связок: x Ù y = 0, а остальные связки Ú , ® , 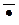 интерпретируем стандартно.
интерпретируем стандартно.
Ясно, что множество “истинных” формул замкнуто относительно правила modus ponens (импликация стандартна).
Схема аксиом (К3) “ложна в рассматриваемой модели”, т.к. принимает значение 0 Ï И при А = В = С = 1. Среди остальных аксиом нужно проверять только схемы (К1) и (К2), которые, очевидно, будут принимать всегда значение 1, т.к. А Ù В = 0 и импликация вычисляется стандартно.
Независимость схемы (Д1): (A ® (A Ú B)) . Проверки аналогичны вычислениям для схемы (К1): берём М = {0, 1}, И = {1}, и для элементов x, y Î M полагаем x Ú y = y, интерпретируя остальные связки Ù , ® , 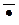 стандартно.
стандартно.
Независимость схемы (Д2): (B ® (A Ú B)) . Докажите самостоятельно, видоизменив интерпретацию дизъюнкции.
Независимость схемы (Д3): ((A ® C) ® ((B ® C) ® (A Ú B ® C))) . Проверки аналогичны вычислениям для схемы (К3): берём М = {0, 1}, И = {1}, и для элементов x, y Î M полагаем x Ú y = 1, интерпретируя остальные связки Ù , ® , 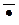 стандартно.
стандартно.
Независимость схемы (О1): (А ® 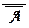 ) . Пусть М = {0, 1, 2}, И = {2} и определим для x, y Î M новые значения логических связок: x Ù y = min{x, y}, x Ú y = max{x, y},
) . Пусть М = {0, 1, 2}, И = {2} и определим для x, y Î M новые значения логических связок: x Ù y = min{x, y}, x Ú y = max{x, y}, 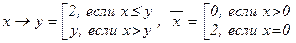 . Проделайте все вычисления самостоятельно.
. Проделайте все вычисления самостоятельно.
Независимость схемы (О2): ( 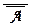 ® А) . Полагаем М = {0, 1, 2}, И = {2} и определим для x, y Î M новые значения логических связок: x Ù y = min{x, y} , x Ú y = max{x, y},
® А) . Полагаем М = {0, 1, 2}, И = {2} и определим для x, y Î M новые значения логических связок: x Ù y = min{x, y} , x Ú y = max{x, y}, 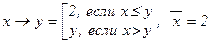 . Проделайте все вычисления самостоятельно.
. Проделайте все вычисления самостоятельно.
Независимость схемы (О3): ((A ® B) ® (  ®
®  )) . Здесь М = {0, 1}, И = {1} и для элемента x Î M новое значение отрицания
)) . Здесь М = {0, 1}, И = {1} и для элемента x Î M новое значение отрицания 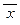 = x , а остальные связки Ù , Ú , ® стандартны. Проделайте все вычисления самостоятельно.
= x , а остальные связки Ù , Ú , ® стандартны. Проделайте все вычисления самостоятельно.
Если рассматривать исчисление высказываний с эквивалентностью, то нужно доказать ещё независимость аксиом эквивалентности (Э1) и (Э2).
Независимость схемы (Э1): ((A « B) ® (( А ® В) Ù (В ® A))) . Нужно взять М = {0, 1}, И = {1} и определить x « y = 1, а все остальные логические связки Ù , Ú , ® интерпретировать стандартно.Проделайте все вычисления самостоятельно.
Независимость схемы (Э2): ((( А ® В) Ù (В ® A)) ® (A « B)) . Нужно взять М = {0, 1}, И = {1} и определить x « y = 0, а все остальные логические связки Ù , Ú , ® интерпретировать стандартно.Проделайте все вычисления самостоятельно.
Теорема о независимости системы аксиом полностью доказана.
Теорема (о независимости аксиом исчисления предикатов).Система аксиом формального исчисления предикатов независима.
Доказательство. Проведём рассуждения схематично. Доказательство независимости схем аксиом исчисления высказываний остаются в силе, если значениям формул (" x A(x)) и ($ x A(x)) с навешенными кванторами вычислять на моделях стандартным образом.
Независимость схемы ("): ((" x А(x)) ® А(t)) . Достаточно интерпретировать логические связки стандартно, как и значения формул с навешенным квантором существования, а формулы с навешенными кванторами всеобщности всегда считать истинными. Тогда, например, аксиома ((" x P(x)) ® P(t)) будет принимать значение 0, если P(t) = 0. Остальные аксиомы при этом останутся тождественно истинными.
Независимость схемы ($): (А(t) ® ( $ x А(x))). Достаточно интерпретировать логические связки стандартно, как и значения формул с навешенными кванторами всеобщности, а формулы с навешенными кванторами существования всегда считать ложными. Тогда, например, аксиома (P(t) ® ($ x P(x))) будет принимать значение 0, если P(t) = 0. Остальные аксиомы при этом останутся тождественно истинными.
Теорема о независимости системы аксиом исчисления предикатов доказана.
§ 6*. Формальное исчисление высказываний
Подробно рассмотрим формальную теорию исчисления высказываний (ИВ). Нашей целью будет обоснование адекватности этой теории, описанной формально в § 1 главы III, неформальной алгебре высказываний, изученной в главе I. Под адекватностью формальной теории её неформальному аналогу понимается доказательство всех основных теорем неформальной теории в соответствующей формальной теории. В частности, будет доказано, что формула доказуема в формальной теории исчисления высказываний тогда и только тогда, когда она тождественно истинна.
1. Свойства выводимости формул.Докажем некоторые основные свойства выводимости формул.
10. Всякая доказуемая формула выводима из любой совокупности формул. В частности, любая аксиома выводима из любой совокупности формул.
Действительно, доказательство формулы является и её выводом из любой совокупности формул, т.к. в нём используются аксиомы и правило вывода modus ponens. Последовательность из одной этой аксиомы является её доказательством.
20. Из любой совокупности выводима любая формула этой совокупности.
В самом деле, если Г = {А1 , … , Аi , … , Аn }, то последовательность из одной формулы Аi является выводом формулы Аi из совокупности Г.
30. Доказуемая формула выводима из любой совокупности формул.
Действительно, доказательство этой формулы является её выводом из любой конечной совокупности формул.
40. Если существует квазивывод формулы В из совокупности Г, т.е. конечная последовательность формул В1 , … , Вk = B, каждая формула которой либо выводима из Г, либо получена из двух предыдущих по правилу modus ponens, то формула В выводима из Г.
Нужно просто заметить, что квазивывод расширится до вывода, если вместо каждой выводимой из Г формулы Вi вставить её вывод из совокупности Г.
50. Если Г  Ф, то для любой совокупности формул D верно Г, D
Ф, то для любой совокупности формул D верно Г, D  Ф.
Ф.
В самом деле, вывод формулы В1 , … , Вk = B из совокупности Г является её выводом и из расширенной совокупности Г, D .
60. Если Г  Ф и Г
Ф и Г  (Ф ® Y), то Г
(Ф ® Y), то Г  Y .
Y .
Действительно, если В1 , … , Вk = Ф – вывод формулы Ф, а С1 , … , Сm = = (Ф ® Y ) – вывод формулы (Ф ® Y ), то В1 , … , Вk = Ф, С1 , … , Сm = = (Ф ® Y ), Y – вывод формулы Y, т.к. последняя формула этой цепочки получена из предыдущих Ф и (Ф ® Y) по правилу modus ponens.
Замечание: На самом деле в свойствах 50 и 60 обоснованы правила вывода 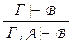 – расширения посылок и
– расширения посылок и 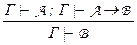 – расширение modus ponens. Теперь ими можно пользоваться при выводе формул, сокращая длину доказательства. Дальнейший ход изложения лишь увеличит количество полезных правил вывода.
– расширение modus ponens. Теперь ими можно пользоваться при выводе формул, сокращая длину доказательства. Дальнейший ход изложения лишь увеличит количество полезных правил вывода.
2. Теорема о дедукции:Обоснуем доказанные в главе I неформально правила дедукции: 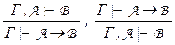 .
.
Теорема (о дедукции).Для формул А, В и произвольной конечной совокупности формул Г (возможно пустой) утверждение Г, А  В имеет место тогда и только тогда, когда Г
В имеет место тогда и только тогда, когда Г  (А ® B).
(А ® B).
Доказательство. Вначале докажем “лёгкую” импликацию (Ü). Если верно Г  (А ® B), то (по правилу расширения посылок) Г, А
(А ® B), то (по правилу расширения посылок) Г, А  (А ® B) и Г, А
(А ® B) и Г, А  А (используется 20). Применяя расширение modus ponens, получим Г, А
А (используется 20). Применяя расширение modus ponens, получим Г, А  В, что и требовалось.
В, что и требовалось.
(Þ) Рассмотрим вывод В1 , … , Вk = В формулы В из совокупности Г, А . Если k = 1, то этот вывод состоит из одной формулы В и возможны случаи:
а: В – аксиома.Тогда цепочка (B ® (A ® B)), B, (A ® B) будет доказательством формулы (A ® B) и выводом её из совокупности Г. Последняя формула цепочки получена из предыдущих по правилу modus ponens.
б: В – формула совокупности Г, А. Если В = А , то (А ® B) = (A ® A) – доказуемая формула (см. пример доказательства в § 1), которая выводима из любого множества формул по свойству 10.Если же В Î Г, то цепочка (B ® (A ® B)), B, (A ® B) является выводом формулы (A ® B) из Г.
Пусть теперь k > 1 и неверно, что Г  (А ® B). Можно считать, что k – наименьшее натуральное число с этим свойством. Таким образом, для любых формул Ф, Y со свойством Г, Ф
(А ® B). Можно считать, что k – наименьшее натуральное число с этим свойством. Таким образом, для любых формул Ф, Y со свойством Г, Ф  Y и длиной этого вывода меньше k будет верно Г
Y и длиной этого вывода меньше k будет верно Г  (Ф ® Y).
(Ф ® Y).
В случаях, когда В – аксиома или формула совокупности Г, А применимы использованные ранее для k = 1 аргументы. Значит можно считать, что последняя формула В рассматриваемого вывода получена из двух предыдущих по правилу modus ponens. Итак, среди формул вывода В есть формулы Вi = C, Bj = (C ® B), где i < k, j < k, т.е. Г, А  С и Г, А
С и Г, А  (C ® B) с длинами выводов, меньшими k. Учитывая предположение о минимальности k, получаем Г
(C ® B) с длинами выводов, меньшими k. Учитывая предположение о минимальности k, получаем Г  (А ® C) и Г
(А ® C) и Г  (А ® (C ® B)). Теперь можно написать квазивывод формулы (А ® B) из множества формул Г :
(А ® (C ® B)). Теперь можно написать квазивывод формулы (А ® B) из множества формул Г :
1· ((A ® (C ® B)) ® ((A ® C) ® (A ® B))) (И2) (А := A, B := C, С := B)
2 ·(A ® (C ® B)) выводима из Г
3 ·((A ® C) ® (A ® B)) МР(1, 2)
4 ·(A ® C)выводима из Г
5 · (A ® B) МР(3, 4)
Теорема о дедукции доказана.
3. Производные правила вывода.Обоснуем некоторые знакомые правила логического вывода. Остальные правила докажите самостоятельно.
Правило перестановки посылок: 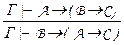 . Запишем квазивывод формулы (В ® (A ® C)), предполагая, что (А ® (В ® C)) выводима.
. Запишем квазивывод формулы (В ® (A ® C)), предполагая, что (А ® (В ® C)) выводима.
1 · Г  (А ® (В ® C))дано
(А ® (В ® C))дано
2 · Г, А  (В ® C) дедукция
(В ® C) дедукция
3 · Г, А, В  С дедукция
С дедукция
4 · Г, В  (А ® C) дедукция
(А ® C) дедукция
5 · Г  (В ® (А ® C)) дедукция
(В ® (А ® C)) дедукция
Правила силлогизма: 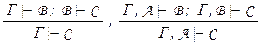 .
.
1 · Г  В дано
В дано
2 · В  С дано
С дано
3 · Г, В  С расширение посылок
С расширение посылок
4 · Г  (В ® С) дедукция
(В ® С) дедукция
5 · Г  СМР(1, 4)
СМР(1, 4)
1 · Г, А  В дано
В дано
2 · Г  (А ® B) дедукция
(А ® B) дедукция
3 · Г, В  С дано
С дано
4 · Г  (В ® С) дедукция
(В ® С) дедукция
5 · ((В ® C) ® (A ® (B ® C)))(И1)(A := (B ® C), B := A)
6 · Г  (A ® (B ® C)) МР(4, 5)
(A ® (B ® C)) МР(4, 5)
7 · ((А ® (B ® C)) ® ((A ® B) ® (A ® C))) аксиома (И2)
8 · Г  ((A ® B) ® (A ® C)) МР(6, 7)
((A ® B) ® (A ® C)) МР(6, 7)
9 · Г  (A ® C) МР(2, 8)
(A ® C) МР(2, 8)
10 · Г, А  C дедукция
C дедукция
Правило объединения посылок: 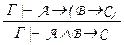 .
.
1 · Г  (А ® (В ® С)) дано
(А ® (В ® С)) дано
2 · Г, А  (В ® С) дедукция
(В ® С) дедукция
3 · ((А ® A) ® ((A ® B) ® (A ® (A Ù B)))) (К3) (A := A =: B, C := B)
4· (A ® A) доказуема
5 · ((A ® B) ® (A ® (A Ù B))) МР(3, 4)
6 · (А Ù В) ® А (К1)
7 · (A Ù B)  A дедукция
A дедукция
8 · Г, (A Ù B)  A расширение посылок
A расширение посылок
9 · Г, (A Ù B)  (В ® С) силлогизм(2, 8)
(В ® С) силлогизм(2, 8)
10 · Г, (A Ù B), В  Сдедукция
Сдедукция
11 · ((A Ù B) ® B)(К2)
12 · (A Ù B)  B дедукция
B дедукция
13· Г, (A Ù B)  Врасширение посылок
Врасширение посылок
14 ·Г, (A Ù B)  Ссиллогизм(10, 13)
Ссиллогизм(10, 13)
15 · Г  ((А Ù B) ® C)дедукция
((А Ù B) ® C)дедукция
Правило разделения посылок: 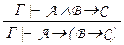 .
.
1 · Г  ((A Ù B) ® C) дано
((A Ù B) ® C) дано
2 · Г, (А Ù B)  C дедукция
C дедукция
3 · Г, А, (А Ù B)  C расширение посылок
C расширение посылок
4 · ((A ® A) ® ((A ® B) ® (A ® (A Ù B)))) (К3)(А := А, В := А, С := В)
5 · (А ® A) доказуема
6 · ((A ® B) ® (A ® (A Ù B))) МР(4, 5)
7 · B, A  В 20
В 20
8 · В  (А ® В) дедукция
(А ® В) дедукция
9 · В  (A ® (A Ù B)) МР(6, 8)
(A ® (A Ù B)) МР(6, 8)
10 · B, A  (A Ù B) дедукция
(A Ù B) дедукция
11 · Г, B, A  (A Ù B) расширение посылок
(A Ù B) расширение посылок
12 · Г, А, В  C силлогизм(3, 11)
C силлогизм(3, 11)
13 · Г, А  (В ® C) дедукция
(В ® C) дедукция
14 · Г  (А ® (В ® C)) дедукция
(А ® (В ® C)) дедукция
Правила удаления конъюнкции: 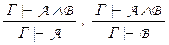 .
.
1 · Г  (A Ù B) дано
(A Ù B) дано
2 · (A Ù B) ® A (К1)
3 · Г  A МР(1, 2)
A МР(1, 2)
Второе правило докажите самостоятельно.
Правила введения конъюнкции: 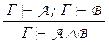 .
.
1 · Г  A дано
A дано
2 · Г  В дано
В дано
3 · Г, А  В расширение посылок
В расширение посылок
4 · Г  (A ® В) дедукция
(A ® В) дедукция
5 · ((А ® A) ® ((A ® B) ® (A ® (A Ù B))))(К3)(А := А, В := А, С := В)
6 · (A ® A) доказуема
7 · ((A ® B) ® (A ® (A Ù B))) МР(5, 6)
8 · Г  (A ® (A Ù B)) МР(4, 7)
(A ® (A Ù B)) МР(4, 7)
9 · Г  (A Ù B) МР(1, 8)
(A Ù B) МР(1, 8)
Правила введения дизъюнкции: 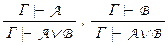 .
.
1 · Г  A дано
A дано
2 · (A ® (A Ú B)) (Д3)
3 · Г  (A Ú В) МР(1, 2)
(A Ú В) МР(1, 2)
Второе правило докажите самостоятельно.
Правило modus tollens:











