Основные операции над множествами

I. Если А, В – множества, то существует множество А È В – объединение множествА и В, которое состоит из всех элементов, являющихся элементами либо множества А, либо множества В: x Î A È B « x Î A Ú x Î B.

Примеры: 1.Если A = {1, 2, 5, Æ}, B = {{1}, 2, 5, Æ}, то А È В = {1, 2, 5, Æ, {1}}.

2. Если A = {x Î R | 1 < x £ 5}, B = {x Î R | –1 £ x < 2}, то A È B = [–1; 5], где [–1; 5] = {x Î R | –1 £ x £ 5}.

II. Если А, В – множества, то существует множество А Ç В – пересечение множествА и В, которое состоит из всех элементов, являющихся одновременно элементами и множества А, и множества В: x Î A Ç B « x Î A Ù x Î B.

Примеры: 1. Если A = {1, 2, 5, Æ}, B = {{1}, 2, 5, Æ}, то А Ç В = {2, 5, Æ}.

2. Если A = {x Î R | 1 < x £ 5}, B = {x Î R | –1 £ x < 2}, то A Ç B = (1; 2), где (1; 2) = {x Î R | 1 < x < 2}.

3. A Ç B = {a Î A | a Î B}.

На основе понятий пересечения и объединения двух множеств можно ввести аналогичные операции над несколькими множествами:

A₁ Ç … Ç A_n = (…((A₁ Ç A₂) Ç A₃) Ç …) Ç A_n ,

A₁ È … È A_n = (…((A₁ È A₂) È A₃) È …) È A_n .

III. Если А, В – множества, то существует множество А \ В – разность множествА и В, которое состоит из всех элементов, принадлежащих множеству А, но не принадлежащих множеству В: x Î A \ B « x Î A Ù x Ï B.

Примеры: 1. Если A = {1, 2, 5, Æ}, B = {{1}, 2, 5, Æ}, то А \ В = {1}.

2. Если A = {x Î R | 1 < x £ 5}, B = {x Î R | –1 £ x < 2}, то A \ B = [2; 5].

3. A \ B = {a Î A | a Ï B}.

IV. Если А – множество, то существует множество всех его подмножествB(A), называемое также булеаном множестваА, и состоящее из всех подмножеств множества А: X Î B(A) « X Í A.

Важно отметить, что булеан B(A) состоит из множеств (подмножество множества А само является множеством) и содержит в качестве элементов пустое множество Æ и само множество А (которые в случае А = Æ совпадают).

Примеры: 1. Если А = Æ, то B(A) = {Æ}.

2.Если A = {1}, то B(А) = {Æ, {1}}.

3. Если A = {1, 2}, то B(А) = {Æ, {1}, {2}, {1, 2}}.

4. Если A = {1, 2, 3}, то B(А) = {Æ, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}.

5.Можно доказать, что булеан n-элементного множества А состоит из 2ⁿ элементов. Поэтому булеан часто называют степенью множестваА и обозначают 2^A.

V. Если А, В – множества, то существует их прямое (декартово) произведениеА´В, состоящее из всех упорядоченных пар(a; b), где а Î А, b Î B:

А´В = {(a; b) | a Î A Ù b Î B}.

Примеры: 1.Если А = {1}, B = {0, 5}, то А´В = {(1; 0), (1; 5)}.

2. Если А = {0, 2}, B = {0, 5}, то А´В = {(0; 0), (0; 5), (2; 0), (2; 5)}.

3. Если множество А состоит из m элементов, а множество В – из n элементов, то можно доказать, что множество А´В состоит из m´n элементов. По этой причине в названии множества А´В используется термин “произведение”. Если А = B, то множество А´А состоит из m² элементов и называется декартовым квадратом множестваА и обозначается через A².

Вслед за декартовым произведением двух можно ввести и декартово произведение A₁ ´ … ´ A_n = ( … ((A₁ ´ A₂) ´ A₃)´ …)´ A_n n множеств A₁ , … , A_n . Множество 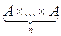называется декартовой степенью множества A и обозначается A ⁿ.

Декартово произведение А´В = {(a; b) | a Î A Ù b Î B} двух множеств А и В иногда условно изображают на плоскости, трактуя компоненты упорядоченной пары (a; b) как координаты: a – координата по оси x, на которой отмечают множество А, а b – координата по оси y, на которой отмечают множество В. Таким образом, элементы (a; b) Î А´B условноизображаютсяточками на плоскости с “координатами” a и b.

Особенно удобно графическое изображение декартова произведения А´В в случае, когда А и В – числовые множества, т.е. А Í R, B Í R . Тогда изображение принимает не условный характер, а имеет вполне конкретный геометрический смысл: множество А´В представляет из себя множество точек M(a; b) декартовой плоскости, первая координата а которых принадлежит множеству А, а вторая b – принадлежит множеству В.