Полнота аксиоматических теорий

Любая содержательная формальная теория строится для обоснования рассуждений в некоторых содержательных теориях. Возникает вопрос: насколько полно описывает формальная теория соответствующую содержательную теорию ? Более точно: насколько тесно связаны понятия истинности формулы в формальной теории и в содержательной ?

Для формальной теории истинность теоремы означает, прежде всего, её доказуемость. Для содержательной теории утверждение истинно, если оно истинно в любой модели данной теории. Таким образом, и для любой формальной теории возникают a’ priori два понимания “истинности” формулы: доказуемость и тождественная истинность (истинность при любой интерпретации рассматриваемой теории).

Интерпретация формальной теории (или модель теории)определяется аналогично введённому выше (см. § 4 главы II) понятию интерпретации для множества формул исчисления предикатов. Не вдаваясь в формальности, ограничимся только намёком: модель теории (или интерпретация) – это некоторое множество вместе с зафиксированными на нём конкретными константами, предикатами и функциями для всех выделенных константных, предикатных и функциональных символов, участвующих в аксиомах теории. При этом требуется, чтобы все аксиомы теории в любой интерпретации этой теории представляли собой истинные в этой модели утверждения.

Если фиксирована интерпретация теории, то любая замкнутая формула теории после замены всех участвующих в ней символов на соответствующие конкретные высказывания, объекты, предикаты и функции этой интерпретации становится высказыванием, которое может быть истинным или ложным. Под замкнутой формулойздесь и далее понимается формула, все вхождения объектных переменных которой связаны. Таким образом, можно говорить об истинности или ложности замкнутой формулы теории на модели теории.

Для незамкнутой формулы A(x₁ , … , x_n) теории со свободными объектными переменными x₁ , … , x_n можно ввести понятие интерпретации формулы теории : это – любая модель теории вместе с фиксированными объектами o₁ , … , o_n для свободных переменных. После замены в этой формуле всех участвующих в ней символов на соответствующие конкретные высказывания, объекты, предикаты и функции модели, а переменных x₁ , … , x_n – на объекты o₁ , … , o_n получится высказывание, которое может быть истинным или ложным. Значит, можно говорить о значениях формулы теории при её интерпретациях, и о тождественно истинных формулах теории – формулах, принимающих значение истина при любой интерпретации. При этом незамкнутая формула A(x₁ , … , x_n) теории со свободными объектными переменными x₁ , … , x_n тождественно истинна тогда и только тогда, когда тождественно истинна замкнутая формула той же теории (" x₁ (" x₂ ( … (" x_n A(x₁ , … , x_n))))).

Замечания: 1. При интерпретации специальной теории все логические связки и кванторы интерпретируются стандартным образом (в соответствии с неформальными аксиомами § 3 главы I и § 1 главы II).

2. При интерпретации формальных теорий исчисления высказываний и предикатов сами истинностные значения логических связок, как и истинностные значения формул, полученных навешиванием кванторов, могут изменяться (подробнее об этом см. § 5).

Ясно, что правила вывода теории предикатов, применённые к тождественно истинным формулам, снова приводят к тождественно истинным формулам. Поэтому любая доказуемая формула специальной теории является тождественно истинной. Таким образом, сформулированный выше вопрос полноты можно поставить так: верно ли, что любая тождественно истинная формула специальной формальной теории доказуема ? Этот вопрос нетривиален даже для формальной теории исчисления предикатов (для формальной теории исчисления высказываний он будет решён положительно (но не просто) в § 6).

Система аксиом формальной теории, как и сама теория, называется полной в широком смысле, если любая тождественно истинная формула этой формальной теории доказуема.

Теорема (о полноте в широком смысле).Любая непротиворечивая специальная теория полна в широком смысле.

Доказательство. Используем (без доказательства) следующую нетривиальную теорему:

Теорема (о существовании модели).Теория непротиворечива тогда и только тогда, когда она имеет модель.

Если теперь А – некоторая недоказуемая, но тождественно истинная формула некоторой специальной теории, то формула также недоказуема: если бы она была доказуема, то была бы истинной в каждой модели, вопреки тождественной истинности формулы А. Более того, присоединение к аксиомам рассматриваемой теории формулы приводит к противоречивой теории: если бы эта новая теория была бы непротиворечива, то у неё существовала бы модель, в которой была бы истинна формула , что невозможно ввиду тождественной истинности формулы А. Итак, существует такое конечное множество Г аксиом исходной теории, что Г, 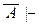Ф и Г, 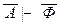. По правилу опровержения 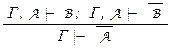отсюда получим Г 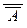, т.е. (с учётом аксиомы 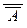® A и правила силлогизма) Г А .

Теорема доказана.

Итак, понятие доказуемости формулы формальной теории совпадает с понятием тождественной истинности. Этот факт укреплял уверенность математиков в том, что программа Гильберта обоснования математики путём формализации приведёт к успеху.

Систему аксиом или саму теорию назовём полной, если для любой замкнутой формулы Ф этой теории доказуема либо сама формула Ф, либо её отрицание 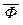. Система аксиом формальной теории, как и сама теория, называется полной в узком смысле, если добавление любой недоказуемой в этой теории замкнутой формулы к списку аксиом теории приводит к противоречивой теории. Наконец, теорию или её систему аксиом назовём ф-категоричной, если для любой её модели множества истинных в этой модели замкнутых формул теории одно и то же. Приведённое определение ф-категоричности не совпадает с общепринятым определением категоричности теории, которое требует понятия изоморфизма моделей, не рассматриваемое в этих лекциях.

Следует отметить, что далеко не каждая содержательная математическая теория полна: утверждение о доказуемости отрицания недоказуемого математического утверждения не верно. Например, утверждение, представляющее аксиому параллельности Евклида (через каждую точку плоскости, не лежащую на заданной прямой, проходит ровно одна прямая, параллельная этой прямой) недоказуемо в системе аксиом абсолютной геометрии, как и его отрицание.

Теорема (о взаимосвязях понятий полноты).Следующие утверждения для любой специальной теории эквивалентны:

(1) теория полна,

(2) теория полна в узком смысле,

(3) теория ф-категорична.

Доказательство.Ясно, что противоречивая теория полна, полна в узком смысле и ф-категорична (?!). Для непротиворечивой теории используем следующую схему доказательства: .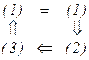

(1) Þ (2) Пусть теория полна, и замкнутая формула Ф не доказуема в этой теории. Тогда доказуема формула 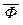, т.е. Г 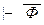, где Г – некоторое конечное множество аксиом теории. Нужно понять, что добавление формулы Ф к списку аксиом приводит к противоречивой теории. Действительно, Г, Ф 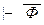и Г, Ф Ф, что и требовалось доказать.

(2) Þ (3) Пусть специальная теория полна в узком смысле, но существует замкнутая формула Ф этой теории, истинная в одной модели этой теории и ложная в другой. Тогда формула Ф недоказуема, т.к. доказуемые формулы не могут быть ложными в моделях, причём добавление к исходной теории недоказуемой замкнутой формулы Ф не привело к противоречивой теории ввиду наличия модели расширенной теории. Это противоречие доказывает (3).

(3) Þ (1) Пусть теория ф-категорична, но Ф – недоказуемая замкнутая формула этой теории, для которой 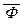также недоказуема. Присоединим недоказуемую формулу 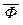к списку аксиом теории.

Если полученная теория будет непротиворечива, то по теореме о существовании модели у неё существует модель, в которой 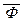истинна. Ввиду ф-кате­горичности 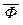тождественно истинна, и по теореме о полноте в широком смысле, 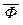доказуема – противоречие.

Если же полученная теория будет противоречива, то существует такое конечное множество Г аксиом теории, что Г, 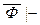А и Г, 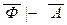для некоторой формулы А. Отсюда по правилу опровержения 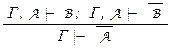получаем Г 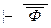, т.е. Ф доказуема (?!) – снова противоречие. Таким образом, либо Ф, либо 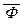доказуема, и теория полна.

Теорема доказана.

Как же обстоит дело со свойством полноты в трёх рассматриваемых модельных формальных теориях исчислений высказываний, предикатов и формальной теории арифметики ?

Для теорий исчисления высказываний и предикатов условие полноты не выполнено, что и неудивительно: это универсальные теории общего назначения, используемые в различных областях знания. Поэтому одна и та же формула (например, формула (a Ú b) исчисления высказываний или формула ($ x P(x)) исчисления предикатов) может быть истинна в одной модели, а в другой ложна. Таким образом, эти теории имеют много различных моделей, отличающихся истинными в них формулами, а потому не полны.

Теорема (о неполноте в узком смысле исчислений высказываний и предикатов).Формальные теории исчисления высказываний и предикатов не полны в узком смысле, не ф-категоричны, но полны в широком смысле.

Упражнения: 1.Докажите, что присоединение к исчислению высказываний в качестве аксиомы формулы x , где х – пропозициональная переменная, приводит к непротиворечивой теории.

2. Докажите, что присоединение к исчислению предикатов в качестве аксиомы формулы ($ x P(x)), где х – объектная переменная, а P(_) – предикатный

символ, приводит к непротиворечивой теории.

3. Докажите, что присоединение к аксиомам формальной арифметики формулы (2´2=5) приводит к противоречивой теории.

Теорема (Линдебаума о пополнении теории).Если специальная теория непротиворечива, то существует её полное непротиворечивое расширение.

Доказательство.Докажем теоерему только в предположении, что все формулы теории можно перенумеровать натуральными числами (т.е. для счётных теорий), хотя её можно доказать и в общем случае, используя трансфинитную индукцию.

Пусть {Ф₁ , Ф₂ , … } – множество всех замкнутых формул рассматриваемой непротиворечивой теории Т. Построим последовательность непротиворечивых теорий Т = Т₀ Í Т₁ Í Т₂ Í … , объединение которых T_∞ = и будет искомой непротиворечивой полной теорией, содержащей исходную теорию Т.

Полагаем Т₀ = Т – непротиворечивая теория. Если уже построена непротиворечивая теория Т_n (n ³ 0) , то для построения теории Т_n+1 рассмотрим формулу . Если эта формула доказуема в теории Т_n , то положим Т_n+1 = Т_n , получая снова непротиворечивую теорию. Если же не доказуема в теории Т_n , то добавим Ф_n+1 к списку аксиом теории Т_n , получая новую теорию Т_n+1 . Эта теория тоже непротиворечива. Действительно, если она противоречива, то любая формула в ней доказуема, в частности, выводима из конечного множества аксиом теории Т_n+1 . Если в этом конечном множестве аксиом отсутствует Ф_n+1 , то доказуема в теории Т_n , что противоречит условию непротиворечивости T_n при построении теории Т_n+1 . Таким образом, для некоторого конечного множества Г аксиом теории Т_n верно Г, Ф_n+1 . Учитывая очевидный факт Г, Ф_n+1 Ф_n+1 ,и применяя правило опровержения 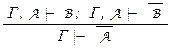, получим Г 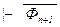– противоречие с построением теории Т_n+1 .

Докажеми теперь, что теория T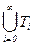_∞ = и будет искомой непротиворечивой полной теорией, содержащей исходную теорию Т. Она непротиворечива ввиду теоремы компактности: если противоречие есть, то оно получается из некоторого конечного списка аксиом, т.е. должно присутствовать и в некоторой теории T_n , что противоречит доказанной непротиворечивости всех теорий T_n (n ³ 0).

Пусть теперь Ф – произвольная замкнутая формула теории T_∞ , являющаяся, конечно, и формулой теории T. Значит Ф = Ф_т для некоторого m Î N, и поэтому представляются следующие возможности: либо доказуема в теории T_m , а значит и в T_∞ , либо недоказуема в теории T_m , но тогда Ф_m является аксиомой теории T_m+1 , доказуема в T_m+1 , а значит и в T_∞ . Таким образом, для любой замкнутой формулы Ф теории T_∞ одна из формул Ф, 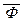доказуема в этой теории.

Теорема о пополнении доказана.

В отличие от формальных теорий исчисления высказываний и предикатов, которые слишком общи, чтобы быть полными, формальная теория арифметики имеет дело с конкретными объектами – натуральными числами, изучаемыми с детства. Поэтому доказанная К. Гёделем в 1931 г. теорема о неполноте арифметики вызвала эффект разорвавшейся бомбы.

Теорема (Гёделя о неполноте формальной арифметики).Если формальная арифметика непротиворечива, то можно указать конкретную замкнутую формулу, которая, как и её отрицание, не доказуемы в формальной арифметике, т.е. формальная арифметика не полна. В качестве такой формулы можно взять, например, формулу, выражающую факт недоказуемости теоремы арифметики (0 ¹ 1) .

Таким образом, натуральные числа, изучаемые в школе – это лишь одна из возможных моделей формальной арифметики. Оказывается, что существует модель формальной арифметики даже на множестве R всех действительных чисел. К сожалению, приходится сделать вывод: аксиомы не могут выразить адекватно все свойства формализуемого математического объекта; полученные модели аксиоматической теории могут иметь свойства, не предусмотренные в аксиомах и далёкие от первоначального замысла их создателя. Теперь математик, пытающийся доказать какую-либо теорему, должен учитывать возможность того, что она, как и её отрицание, могут быть недоказуемыми в рамках аксиоматики изучаемой теории.

Заметим ещё, что упомянутая в прошлом параграфе обобщённая теоерема Гёделя о неполноте не противоречит теореме о пополнении: просто полное непротиворечивое расширение арифметики (как и любой конструктивно аксиоматизируемой теории, о которой идёт речь) уже не будет конструктивно аксиоматизируемым. Причина этого кроется в том, что, не всегда возможно эффективно определить, доказуема ли в данной теории заданная замкнутая формула.