Непротиворечивость аксиоматических теорий

Система аксиом формальной теории, как и сама теория, называются непротиворечивой, если не существует такой формулы Ф этой формальной теории, что Ф и 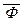доказуемы. При исследовании непротиворечивости теории полезно учитывать следующую теорему:

Теорема (компактности). Система аксиом специальной теории непротиворечива тогда и только тогда, когда непротиворечива любая её конечная подсистема.

Доказательство. Ясно, что из непротиворечивости системы аксиом следует непротиворечивость и любой конечной подсистемы аксиом.

Обратно, пусть непротиворечива каждая конечная подситема системы аксиом, но сама теория противоречива. Тогда из системы аксиом выводятся формулы Ф и :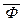

1 ·доказательство формулы Ф 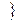Г₁

2 · Ф

3 · доказательство формулы 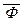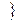Г₂

4 ·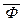

Таким образом, Г 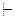Ф и Г 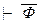, где Г = Г₁ È Г₂ – конечное множество.

Теорема доказана.

По сути дела эта теорема обращает внимание на свойство конечности математических рассуждений.

Требование непротиворечивости является основным для каждой содержательной теории. Дело в том, что если теория противоречива, т.е. исходя из её аксиом с помощью допустимых в ней правил вывода можно доказать формулы Ф и 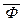, то можно доказать и любую другую формулу. Формальное доказательство этого факта будет дано в § 6, где будут обоснованы доказанные в § 7 главы I правила вывода, а пока воспользуемся доказанными неформально правилами вывода расширения посылок 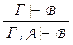и modus tollens: 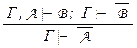. С их помощью дополним доказательства формул Ф и 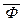до доказательства произвольной формулы A: ввиду теоремы компактности, Г 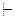Ф и Г 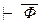, где Г – некоторое конечное множество аксиом. По правилу расширения посылок, Г, 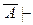Ф, и по правилу modus tollens, Г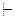 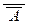. Отсюда легко вывести Г 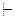А :

·

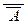
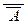· ® А (аксиома)

·А (МР)

Хотя проведённое доказательство и не вполне формальное, но его можно формализовать, используя результаты следующего параграфа.

Таким образом, в противоречивой теории все формулы доказуемы, и сама такая теория не представляет интереса.

Теорема (о непротиворечивости формального исчисления высказываний).Формальное исчисление высказываний непротиворечиво.

Доказательство. Нетрудно проверить, что все аксиомы формального исчисления высказываний представляют из себя тождественно истинные формулы. Кроме того, по правилу modus ponens 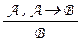разрешается получать формулу В из уже доказанных, а потому (можно считать) тождественно истинных формул А и А ® B . Легко понять, что и сама формула В в этом случае будет тождественно истинной.

Таким образом, все доказуемые в формальном исчслении высказываний формулы являются тождественно истинными. Значит, если доказуема формула Ф, то формула 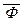доказуемой быть не может, поскольку тождественно ложна.

Теорема доказана.

Теорема (о непротиворечивости формального исчисления предикатов).Формальное исчисление предикатов непротиворечиво.

Доказательство этой теоремы можно получить по той же схеме, что и доказательство предыдущего результата, если аналогично предыдущему обратить внимание на то, что в формальной теории предикатов доказуемы только тождественно истинные формулы: все аксиомы тождественно истинны, а применение правил вывода modus ponens и введения кванторов 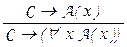, 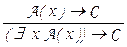не выводит за пределы тождественно истинных формул. Таким образом, любая выполнимая формула не может быть доказана в формальной теории предикатов.

Теорема доказана.

Эта теорема Гёделя, доказанная в 1930 г. XX в., обосновывалась им, почти не опираясь на аксиоматику теории множеств, чего не скажешь о приведённом выше коротком доказательстве этой теоремы. Дело в том, что оно использует понятие тождественно истинной формулы, которое оперирует понятием интерпретации, базирующимся, в свою очередь, на понятиях множества и предиката, т.е. использует аксиомы и некоторые нетривиальные факты теории множеств. Таким образом, приведённые доказательства теорем о непротиворечивости не являются формальными доказательствами в рамках самих формальных теорий исчисления высказываний и предикатов.

Всё-таки полученные доказательства непротиворечивости простейших математических теорий вселяли надежду на то, что вскоре удастся формальными методами доказать непротиворечивость других, более содержательных, математических теорий, а затем, быть может, и всей математики. Такова была программа Д. Гильберта формального обоснования математики. Однако, этим надеждам не суждено было сбыться: в 1931 г. К. Гёдель доказал, что непротиворечивость формальной арифметики не может быть доказана средствами этой формальной теории, так же как и непротиворечивость любой конструктивно аксиоматизируемой содержательной теории, включающей в себя теорию формальной арифметики. Более точно, результат К. Гёделя формулируется так:

Теорема (обобщённая теорема Гёделя о неполноте). Если конструктивно аксиоматизируемая формальная теория включает в себя формальную арифметику и непротиворечива, то можно указать конкретную формулу этой теории, которая, как и её отрицание, не доказуемы в рассматриваемой формальной теории. В качестве такой формулы можно взять, например, формулу, выражающую факт недоказуемости теоремы арифметики (0 ¹ 1) в этой формальной теории, т.е. непротиворечивость этой формальной теории.

Использованный здесь термин “конструктивно аксиоматизируемая теория” не является общепринятым, подробно его обсуждать не будем. Отметим только, что в такой теории можно все её формулы так эффективно занумеровать натуральными числами, что будет существовать эффективный алгоритм, определяющий по заданному номеру формулы, является эта формула аксиомой теории или нет. Кроме того, существует аналогичная эффективная нумерация правил вывода такой теории, и утверждение о доказуемости любой формулы само записывается в виде формулы. Эти условия выполнены, например, для теории формальной арифметики и для многих других естественно возникающих теорий. Точную формулировку, доказательство и комментарии к теореме Гёделя можно найти в книге [12 ниже, стр. 67-79].

Таким образом, реализация программы формализации математики оказалась невозможной: в рамках содержательной формальной теории нельзя обосновать непротиворечивость этой теории. Это не исключает возможности обоснования этой теории средствами какой-либо более широкой теории. Однако обоснование непротиворечивости этой более широкой теории требует нового расширения теории, и.т.д. Например, непротиворечивость формальной арифметики была обоснована Г. Генценом, используя трансфинитную индукцию, применяемую в теории множеств (см. § 2 приложения). Но обоснование непротиворечивости самой теории множеств требует выхода уже за рамки теории множеств.