Плоскопараллельное движение тела
Движение твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости, называется плоскопараллельным.
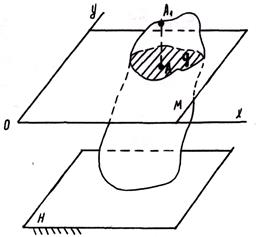
Изучая плоскопараллельное движение тела М, достаточно рассматривать движение его плоского сечения q плоскости ХОУ.
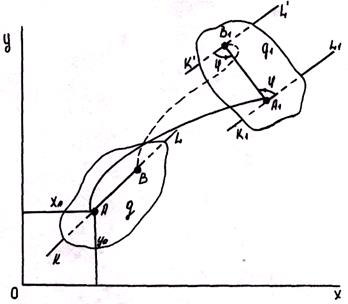
Выберем в сечении q произвольную точку A, которую назовем полюсом. Свяжем с полюсом А некоторую прямую KL , а в самом сечении вдоль прямой KL проведем отрезок AB, перемещая плоское сечение из положения q в положение q1. Можно сначала передвинуть его вместе с полюсом А поступательно, а затем повернуть на угол 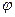 .
.
Плоскопараллельное движение тела – движение сложное и состоит из поступательного движения вместе с полюсом и вращательного движения вокруг полюса.
Закон плоскопараллельного движения можно задать тремя уравнениями:
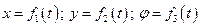 .
.
Дифференцируя заданные уравнения плоскопараллельного движения, можно в каждый момент времени определить скорость 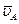 и ускорение
и ускорение 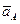 полюса, а также угловую скорость
полюса, а также угловую скорость 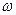 и угловое ускорение
и угловое ускорение 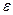 тела.
тела.
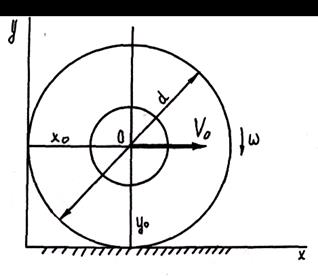
Пусть, например, движение катящегося колеса диаметром d задано уравнениями 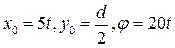 , где
, где 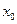 и
и 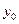 – м,
– м, 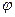 – рад, t – с. Продифференцировав эти уравнения, находим, что скорость полюса O
– рад, t – с. Продифференцировав эти уравнения, находим, что скорость полюса O 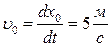 , угловая скорость колеса
, угловая скорость колеса 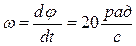 . Ускорение полюса и угловое ускорение колеса в данном случае равны нулю. Зная скорость полюса и угловую скорость тела, можно затем определить скорость любой его точки.
. Ускорение полюса и угловое ускорение колеса в данном случае равны нулю. Зная скорость полюса и угловую скорость тела, можно затем определить скорость любой его точки.
8.3. Определение скорости любой точки тела
при плоскопараллельном движении
Пусть дано плоское сечение q , угловая скорость и скорость полюса которого в некоторый момент времени соответственно 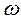 и
и 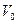 . Требуется определить скорость какой-либо точки А.
. Требуется определить скорость какой-либо точки А.
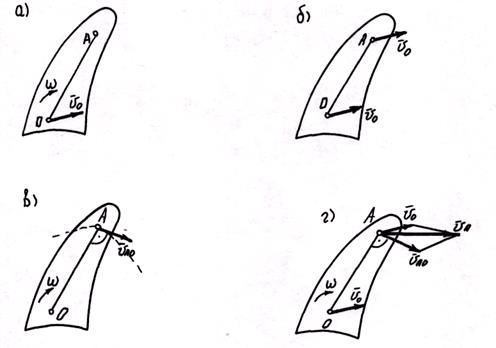
Расчленим плоскопараллельное движение на составные части – поступательную и вращательную. При поступательном движении вместе с полюсом (переносное движение) все точки сечения, и точка А в том числе, имеют переносную скорость 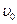 , равную скорости полюса. Одновременно с поступательным сечение q, совершает вращательное движение с угловой скоростью
, равную скорости полюса. Одновременно с поступательным сечение q, совершает вращательное движение с угловой скоростью 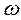 (относительное движение).
(относительное движение).
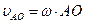 ,
,
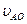 – относительная скорость точки A (
– относительная скорость точки A ( 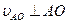 ).
).
Следовательно, в каждый данный момент времени
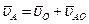 ,
,
т.е. абсолютная скорость точки тела при плоскопараллельном движении равна геометрической сумме скорости полюса и относительной скорости этой точки вокруг полюса.
Модуль абсолютной скорости может быть определен по формуле
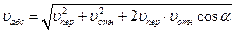 ,
,
а направление – с помощью теоремы синусов. Если же направление абсолютной скорости известно, то ее модуль определяется проще на основании следующей теоремы: проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, равны между собой.
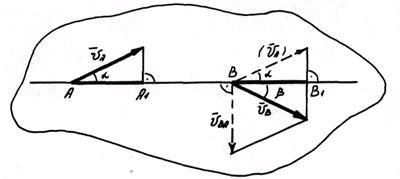
Допустим, что известны скорости 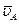 и
и 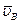 точек A и В какого-либо тела. Приняв за полюс точку A, получим
точек A и В какого-либо тела. Приняв за полюс точку A, получим
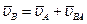 .
.
Относительная скорость 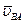 перпендикулярна АВ. Следовательно,
перпендикулярна АВ. Следовательно, 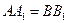 или
или 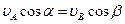 . Теорема доказана.
. Теорема доказана.
Дата добавления: 2021-12-14; просмотров: 464;











