Скорости и ускорения различных точек вращающегося тела
Определим скорость и ускорение любой точки в любой момент времени. Для этой цели установим зависимость между угловыми величинами 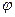 ,
, 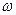 и
и 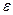 , характеризующими вращательное движение тела, и линейными величинами
, характеризующими вращательное движение тела, и линейными величинами 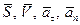 и
и 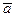 , характеризующими движение точек тела.
, характеризующими движение точек тела.
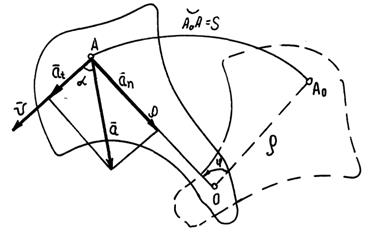
Допустим, что тело, показанное на рисунке, вращаемся согласно уравнению 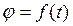 . Требуется определить скорость
. Требуется определить скорость 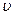 и ускорение
и ускорение 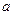 точки А этого тела, расположенной на расстоянии от оси вращения O. Пусть тело за некоторое время tповернулось на угол
точки А этого тела, расположенной на расстоянии от оси вращения O. Пусть тело за некоторое время tповернулось на угол 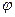 , а точка А, двигаясь по окружности из некоторого начального положения
, а точка А, двигаясь по окружности из некоторого начального положения 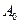 , переместилась на расстояние
, переместилась на расстояние 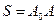 . Так как угол
. Так как угол 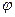 выражается в радианах, то
выражается в радианах, то
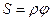 (7.9)
(7.9)
т.е. расстояние, пройденное точкой вращающегося тела, пропорционально его углу поворота. Расстояние S и угол поворота 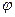 – функции времени, a
– функции времени, a 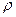 – величина, постоянная для данной точки. Продифференцируем по времени обе части равенства (7.9) и получим
– величина, постоянная для данной точки. Продифференцируем по времени обе части равенства (7.9) и получим
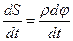
но 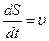 – скорость точки, a
– скорость точки, a 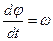 – угловая скорость тела, поэтому
– угловая скорость тела, поэтому
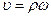 (7.10)
(7.10)
т.е. скорость точки вращающегося тела пропорциональна его угловой скорости.
Изформулы (7.10) видно, что для точек, расположенных на оси вращения, 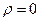 и скорости этих точек также равны нулю. По мере изменения
и скорости этих точек также равны нулю. По мере изменения 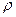 , т.е. у точек, находящихся дальше от оси вращения, скорости тем больше, чем больше значение
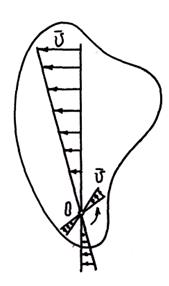
, т.е. у точек, находящихся дальше от оси вращения, скорости тем больше, чем больше значение 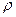 . Пропорциональная зависимость скоростей различных точек вращающегося тела от их расстояний относительно оси вращения показана на рисунке.
. Пропорциональная зависимость скоростей различных точек вращающегося тела от их расстояний относительно оси вращения показана на рисунке.
Продифференцировав обе части равенства (7.10), имеем
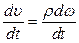 ,
,
но 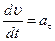 – касательное ускорение точки, a
– касательное ускорение точки, a 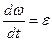 – угловое ускорение тела, значит
– угловое ускорение тела, значит
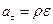 (7.11)
(7.11)
т.е. касательное ускорение точки вращающегося тела пропорционально его угловому ускорению.
Подставив в формулу 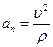 , значение скорости из формулы (7.10), получим
, значение скорости из формулы (7.10), получим
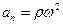 (7.12)
(7.12)
т.е. нормальное ускорение точки вращающегося тела пропорционально второй степени его угловой скорости.
Из формулы 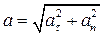 после подстановки вместо
после подстановки вместо 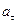 и
и 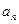 их значений из формул (7.11) и (7.12) получаем
их значений из формул (7.11) и (7.12) получаем
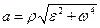 (7.13)
(7.13)
Направление вектора ускорения, т.е. угол 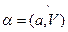 , определяется по одной из формул
, определяется по одной из формул  , причем последнюю из них можно представить теперь в таком виде:
, причем последнюю из них можно представить теперь в таком виде:
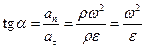 (7.14)
(7.14)
Из формул (7.13) и (7.14) следует, что для точек тела при его вращательном движении по заданному закону можно сначала найти ускорение  , а затем разложить его на касательное ускорение
, а затем разложить его на касательное ускорение 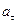 и нормальное ускорение
и нормальное ускорение 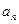 , модуль которых
, модуль которых
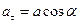 и
и 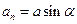
Дата добавления: 2021-12-14; просмотров: 579;











