Сложное движение точки

Примером сложного движения точки может служить:

а) лодка (если ее принять за материальную точку), плывущая от одного берега реки к другому;

б) шагающий по ступенькам движущегося эскалатора в метро че­ловек также совершает сложное движение относительно неподвижного свода туннеля.

Таким образом, при сложном движении точка, двигаясь относи­тельно некоторой подвижной материальной среды, которую условимся называть подвижной системой отсчета, одновременно передвигается вместе с этой системой отсчета относительно второй системы от­счета, условно принимаемой за неподвижную.

Движение некоторой точки М по отношению к подвижной системе отсчета называется относительным. Движение подвижной системы от­счета вместе со всеми связанными с ней точками материальной сре­ды по отношению к неподвижной системе отсчета называется для точки М переносным. Движение точки М по отношению к неподвижной системе отсчета называется сложным, или абсолютным.

Для того чтобы видеть сложное (абсолютное) движение точки, наблюдатель должен сам быть связан с неподвижной системой отсче­та. Если же наблюдатель находится в подвижной системе отсчета, то он видит лишь относительную часть сложного движения.

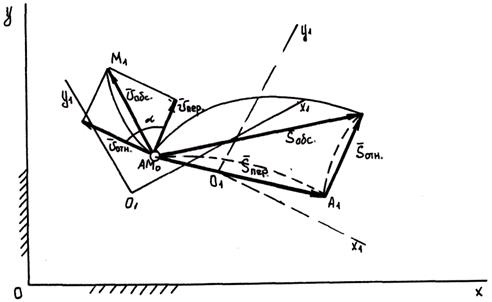
Представим, что точка М переместилась за некоторое время от­носительно подвижной системы координат 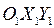из начального по­ложения M₀ в положение М₁ по траектории M₀М₁ (траектории относительного движения точки). За это же время 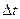подвижная система координат O₁X₁Y₁ вместе со всеми неизменно связанными с ней точ­ками, а значит, и вместе с траекторией относительного движения точки М переместилась в неподвижной системе координат ОХУ в но­вое положение.

Разделим обе части этого равенства на время движения :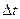

и получим геометрическую сумму средних скоростей:

,

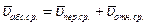которые направлены вдоль соответствующих векторов перемещений. Если теперь перейти к пределам при 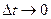, то получим

,

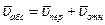выражающее теорему сложения скоростей: при сложном движении точ­ки абсолютная скорость в каждый момент времени равна геометри­ческой сумме переносной и относительной скоростей.

Если задан угол 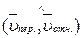, то модуль абсолютной скорости

.

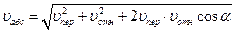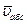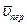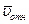Углы, образуемые векторами абсолютной скорости с век­торами и , определяются по теореме синусов.

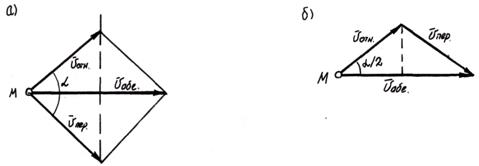
В частном случае при 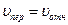при сложении этих скоростей образуется ромб или равнобедренный треугольник и, следовательно,

.