Частные случаи вращательного движения
1. Равномерное вращательное движение. Если угловое ускорение 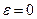 и, следовательно, угловая скорость
и, следовательно, угловая скорость
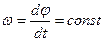 , (7.1)
, (7.1)
то вращательное движение называется равномерным. Из выражения (7.1) после разделения переменных
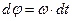 .
.
Если при изменении времени от 0 до t угол поворота изменялся от 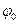 (начальный угол поворота) до
(начальный угол поворота) до 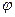 , то, интегрируя уравнение в этих пределах
, то, интегрируя уравнение в этих пределах
 ,
,
получаем уравнение равномерного вращательного движения
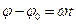 ,
,
которое в окончательном виде записывается так:
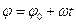 (7.2)
(7.2)
Если 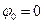 , то
, то
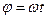 (7.3)
(7.3)
Таким образом, при равномерном вращательном движении угловая скорость
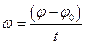 или при
или при 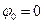
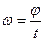
2. Равнопеременное вращательное движение. Если угловое ускорение
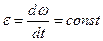 , (7.4)
, (7.4)
то вращательное движение называется равнопеременным. Производя разделение переменных в выражении (7.4):

и приняв, что при изменении времени от 0 до t угловая скорость изменилась от 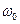 (начальная угловая скорость) до
(начальная угловая скорость) до 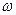 , проинтегрируем уравнение в этих пределах:
, проинтегрируем уравнение в этих пределах:
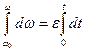 или
или 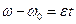
т.е. получим уравнение
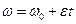 (7.5)
(7.5)
выражающее значение угловой скорости в любой момент времени.
Закон равнопеременного вращательного движения 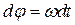 или, с учетом уравнения (7.5):
или, с учетом уравнения (7.5):

Полагая, что в течение времени от 0 до t угол поворота изменялся от 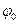 до
до 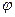 , проинтегрируем уравнение в этих пределах:
, проинтегрируем уравнение в этих пределах:
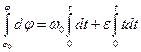 или
или 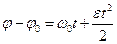
Уравнение равнопеременного вращательного движения в окончательном виде:
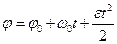 . (7.6)
. (7.6)
Первую «вспомогательную формулу получим» исключив из формул (7.5) и (7.6) время:
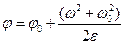 (7.7)
(7.7)
Исключив из тех же формул угловое ускорение 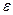 , получим вторую вспомогательную формулу:
, получим вторую вспомогательную формулу:
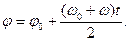 , (7.8)
, (7.8)
где 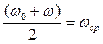 – средняя угловая скорость при равнопеременном вращательном движении.
– средняя угловая скорость при равнопеременном вращательном движении.
Когда 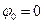 и
и 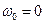 , формулы (7.5), (7.6), (7.7) и (7.8) приобретают более простой вид:
, формулы (7.5), (7.6), (7.7) и (7.8) приобретают более простой вид: 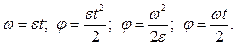
В процессе конструирования угловое перемещение выражают не в радианах, а просто в оборотах.
Угловая скорость, выражаемая количеством оборотов в минуту, называется частотой вращения и обозначается n. Установим зависимость между 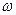 (рад/с) и n (об/мин). Так как
(рад/с) и n (об/мин). Так как 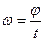 , то при n (об/мин) за t = 1 мин = 60с угол поворота
, то при n (об/мин) за t = 1 мин = 60с угол поворота 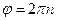 . Следовательно,
. Следовательно,
 .
.
При переходе от угловой скорости 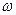 (рад/с) к частоте вращения n (об/мин) имеем
(рад/с) к частоте вращения n (об/мин) имеем
 .
.
Дата добавления: 2021-12-14; просмотров: 584;











