Евристичні методи оптимізації

Розглянемо зміст деяких спеціальних методів, застосовуваних у процесі оптимізації топології ІМ. Для їхньої реалізації необхідно мати обчислювальну систему з більшими ресурсами пам'яті й швидкодією, на базі якої будується система автоматизації топологічного проектування.

Оптимізація топології з використанням евристичних методів виробляється за алгоритмом, що ґрунтується на методі усунення ребер (МУР). Відповідно до цього алгоритму:

1) вибирають вихідну топологію (часто на практиці вибирають повнозв'язну мережу);

2) для кожного каналу, заданого у вихідній топології, проводять статечну апроксимацію вартості: , ;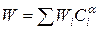

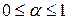3) розглянутими методами вирішують спільне завдання вибору пропускних здатностей і розподілу потоків;

4) задаються дискретними змінами безперервних пропускних здатностей, отриманих з рішення завдання;

5) проводять оптимізацію потоків шляхом застосування алгоритму обмеження потоків;

6) повторюють п. 3 і 5 для ряду реалізованих початкових потоків;

7) при необхідності повторюють п. 1...6 для декількох початкових топологій.

При постановці завдання задають загальне число вузлів, їхнього місця розташування, а в процесі рішення оцінюють характеристики мереж за багатьма варіантами вибору ліній зв'язку між вузлами [6]. Вони формуються шляхом змін вихідних топологічних структур.

На рис. 12 наведена загальна схема алгоритму автоматизованого топологічного проектування із застосуванням ЕОМ. У блоці А генеруються початкові конфігурації, які проходять топологічну перевірку у блоці В. Приймаються рішення про подальші локальні виправлення, за якими іде певна послідовність тестів для пошуку найкращої конфігурації.

Для обраних маршрутів і заданих пропускних здатностей ліній оцінюються транзитні затримки, причому трафік пропорційно збільшується доти, поки максимальна затримка не досягне певного припустимого значення Т_т1п. У блоці Р с обліком річної вартості ліній, що відносять до загального трафіку, підраховується міра економічності, що дорівняє найкращим значенням, отриманим раніше. Закінчення процесу оптимізації визначається часом, відведеним для розрахунків.

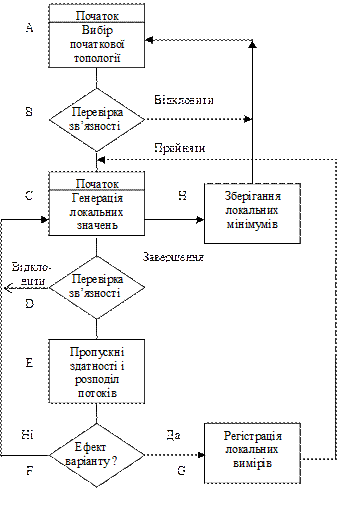
Рисунок 12 - Структурна схема процедури автоматичного

топологічного проектування

Топологічне проектування, і особливо оптимізація мереж, є, як видно з наведених прикладів, складним завданням. Загальних методів її рішення, очевидно, не може бути знайдено, хоча існують різні приватні рішення, засновані на певних допущеннях. У ході рішень широко застосовується обчислювальна техніка, причому можуть знадобитися дуже значні обчислювальні ресурси, які розроблювач не завжди має. Тому застосовують неформалізовані евристичні алгоритми й процедури, отримані шляхом творчого пошуку, інтуїції й досвіду дослідника. Серед відомих евристичних методів можна вказати прийом, який полягає в тому, що інформаційні потоки між парами абонентів мережі направляються найменш завантаженими шляхами з мінімальним числом проміжних вузлів. Такий прийом, як правило, дає результат, що небагато відрізняється від оптимального рішення, одержуваного методами цілочисленого програмування.

Відома також процедура розподілу потоків, що може бути виконана відповідно до методу насичення перетину. Він полягає у наступному (рис. 13). Спочатку шляхами з мінімальним числом вузлів одночасно направляються максимально можливі для всіх пар вузлів потоки. Ці шляхи для кожної пари є «найкоротшими шляхами». «Насичені» лінії 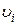, 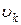(рис. 13, а), що визначають найкоротші шляхи, зі схеми мережі виключаються, а потоки направляються за лініями підмережі, що залишилася, які відповідають найкоротшим шляхам, наприклад 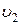, 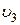(рис. 13, б). Цей процес триває доти, поки зі схеми мережі не буде вилучено стільки ліній, що вона виявиться роз'єднаною (рис. 13, в).

в

б

а

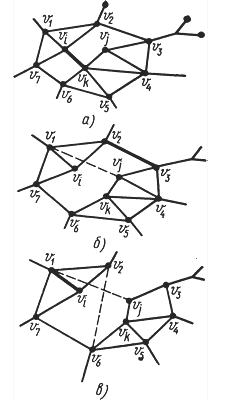
Рисунок 13 - Ілюстрація методу «насичення перетину»

Часто буває необхідно побудувати мережу мінімальної вартості, таку, щоб між вузлами v_i і v_j було хоча б r_ij не пересічних у вузлах шляхів. Остання умова задається спеціальною матрицею надмірності 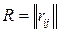, у якій вказуються необхідні для його виконання зв'язку. Число змінних і умов обмеження виявляється дуже велико навіть для порівняно невеликих мереж. Оптимізація полягає у пошуку топології мереж не мінімальної, а зниженої вартості, тобто у пошуку локального мінімуму. Рішення базується на методі заміни галузей, що також є евристичним.

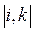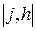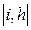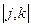Нехай у мережі є дві галузі й , а галузі й у мережі відсутні. Шляхом вилучення галузей 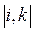і 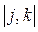й додавання галузей 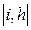і 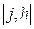можна побудувати нову мережу, якою перевіряється умова: .

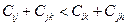Якщо нова мережа буде мати меншу вартість, чим вихідна, то результат заміни приймається. Заміна галузей мережі може порушити вимоги розробки відносно зменшення надмірності між вузлам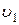и й 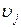. Тоді запропоноване рішення відхиляється. Таким чином, у процесі оптимізації методом заміни проводиться перевірка на відповідність умовам зв’язності для всіх вузлів мережі.

Гарною евристичною процедурою є процедура, реалізована за методом виключення замкнутих шляхів. Вихідною топологією служить довільне дерево (рис. 14, а). За допомогою відповідних перетворень можна одержати з одного дерева будь-яке інше. Ці перетворення полягають у наступному. У даному дереві вибирають вузол 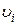і знаходять вузол 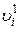, найближчий до 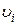, але ще не з'єднаний з ним (рис. 14, б). До вихідного дерева додається галузь 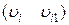і створюється замкнутий ланцюг, що складається з галузей , .

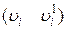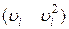Почерговим виключенням галузей 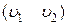, ,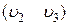…, 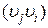утворяться нові дерева (рис. 14, в). На кожному кроці ітерації вирішується завдання оптимального розподілу пропускних здатностей галузей, визначається відповідна вартість мережі й робиться необхідне додавання галузей між вузлам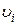и й 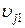, найближчими до 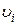,вузлами, для утворення дерев з більше низькою вартістю. Процес триває доти, поки не будуть досягнуті прийнятні варіанти. Для більшості завдань гарні результати виходять при кількості ітерацій 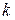, яка дорівнює трьом [6].

в

б

а

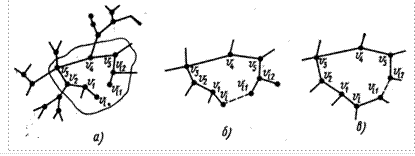
а - вихідна структура; б, в - варіанти ітерацій

Рисунок 14 - Ілюстрація методу «виключення замкнутих шляхів»

Розглянуті ітераційні процедури, що використають евристичні алгоритми, спочатку застосовувалися для оптимізації централізованих топологічних структур. Однак з деякими додатковими прийомами вони виявляються застосовні й для оптимізації децентралізованих мереж. Задається вихідна топологія, а потім у ході простих ітерацій, подібних тим, що були описані для централізованих ІМ, вона модифікується доти, поки не буде отриманий варіант із більше низькою вартістю, що задовольняє всім покладеним обмеженням.

Послідовність модифікацій топологічної структури являє собою деякий клас замін, що полягають у виключенні або додаванні галузей до цієї структури, причому вони можуть уводитися або вилучатися з будь-якого місця в мережі.

Для мереж, структура яких містить контури, завдання проектування в її загальному виді спрощуються. Фізична структура мережі, топологія якої містить ланцюги й контури, звичайно відповідає конфігурації, що складається з декількох терміналів з буферними ЗУ й однієї або декількох ЕОМ, зв'язаних між собою. Завдання оптимізації топологічної структури даного типу полягає у розподілі потоку, що відповідає найменшій вартості. При постійному числі терміналів в ЕОМ розглянуте завдання може бути вирішена за два незалежних етапи: вибір швидкості передачі в ланцюзі на основі міркувань, пов'язаних з обмеженнями на довжину черг (мінімальні затримки в кільці); оптимізація структури ланцюга методом заміни галузей.

У цьому випадку зміст відповідає так званому «завданню комівояжера», що являє собою наступне.

Нехай заданий граф G(V,U), дугам якого приписані різні ваги 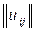. Необхідно знайти такий контур гамільтона, що має найменшу загальну вагу, тобто мінімальний контур гамільтона. Для рішення завдання знаходження мінімального контуру гамільтона користуються алгоритмом Литтла.

Багатоконтурні системи менш економічні в порівнянні з деревоподібними, однак при вимогах надійності оптимальний варіант може відповідати багатоконтурній структурі.

З іншого боку, багатоконтурні системи, у яких потрібно вибрати місце розташування пристроїв у кожному з контурів, є прикладом завдань «групування», і оптимізація таких структур може бути досягнута в рамках завдань при р-медіані.

Наведемо приклад оптимізації розподіленої мережі. На рис. 15, а зображена вихідна мережа, а на рис. 15, б - зазначені виключаючі гілки та гілки, що додають.

а

б

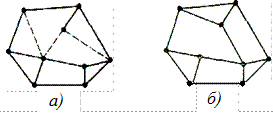
Рисунок 15 - Приклад оптимізації багатоконтурних структур

у рамках завдання при р-медіані

Зі збільшенням розмірів мережі з'являється необхідність у розбивці структури мережі на окремі частини й потрібні додаткові евристичні прийоми. У цей час зазначені методи можна використати для побудови щодо невеликих мереж зі структурами загального виду, що містять кілька сотень вузлів. Однак для мереж великого розміру знадобляться інші процедури.