Критерії й обмеження у завданнях оптимізації ІМ

Розглянуті положення класичної теорії оптимізації лінійного й динамічного програмування є основою для постановки й вибору методів рішення завдань оптимізації ІМ. Принципово можлива постановка нескінченної безлічі оптимізаційних завдань і їхніх модифікацій, розглянутих щодо різноманітних критеріїв, змінних і характеристик інформаційних мереж.

Як критерій часто виступає повна вартість мережі W.

Для лінійної моделі вартості отримане співвідношення, що визначає оптимальне значення пропускної здатності каналів ІМ, у той час як для нелінійної моделі (увігнутої функції) вартості рішення оптимізаційного завдання часто дає кілька локальних мінімумів, що значно ускладнює рішення завдань оптимізації ІМ. Одним з розглянутих критеріїв оптимізації ІМ є надійність інформаційної мережі.

Надійність мережі визначається як здатність забезпечувати нормальний зв'язок між усіма діючими парами вузлів, хоча б одним шляхом. При проектуванні може бути поставлена вимога про необхідність зв'язку між будь-якими парами вузлів за двома і більше незалежними шляхами. Таким чином, кількісним показником надійності, необхідним для оптимізації ІМ, у цих випадках може служити середня частка пар вузлів, між якими зв'язок стає неможливим через ушкодження вузлів або ліній. Для розрахунку цього показника потрібно знати або оцінити інтенсивність відмов елементів, потоки відмов і відновлень окремих ліній і вузлів ІМ.

При постановці оптимізаційного завдання встановлюються обмеження, обумовлені фізичною сутністю процесів, що протікають у досліджуваній мережі, економічними вимогами й іншими конкретними особливостями, наприклад надійністю й ефективністю функціонування елементів.

Інтерес викликають лише деякі з них, наприклад: характеристики топологічних структур ІМ - безліч вузлів N і безліч зв'язків між ними М; пропускні здатності каналів зв'язку, причому кожному зв'язку (дузі) відповідає пропускна здатність 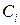. Це найчастіше дискретна, а рідше безперервна змінна. Кожному значенню 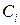буде відповідати вартість .

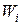Відомі дві моделі, що встановлюють взаємозв'язки W і З (рис. 11): лінійна 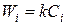й статечна (увігнута) і 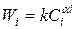. Вартість каналів також є або безперервної, або дискретною величиною. Загальна вартість мережі

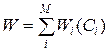
часто фігурує як змінна в завданнях оптимізації ІМ.

Загальноприйнятим критерієм, що оцінює якість функціонування, є середня затримка повідомлень Т:

,

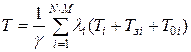де 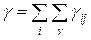- загальна пропускна здатність мережі; 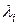- частота появи повідомлень у 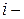м каналі; 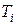- середній час на передачу повідомлень плюс час очікування для 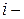го каналу; 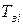- час затримки проходження повідомлень по 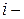му каналі; 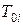- час обробки у вузлі, розташованому за 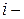м каналом.

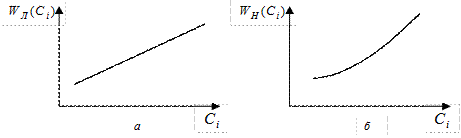
а — лінійна; б — увігнута

Рисунок 11 - Види аналітичних залежностей для моделей вартості каналів зв'язку ІМ у функції від пропускної здатності

Серед обмежень, що мають місце у завданнях оптимізації ІМ, зазначаються наступні.

1 Обмеження на потік. При збереженні потоку у вузлах для кожної сукупності 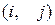дуг не має бути втрат і розсіювання його на цих дугах, тобто

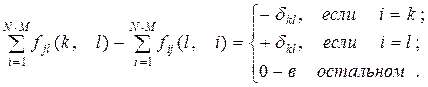
2 Обмеження на пропускну здатність каналів зв'язку, що виражає реальна властивість передавати обмежена кількість інформації за одиницю часу:

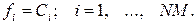
3 Обмеження на вартості визначається кінцевими фінансовими ресурсами, виділюваними на створення мережі (планований бюджет):

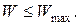
4 Обмеження на затримку передачі повідомлень. Фактор затримки може бути визначений фізичними причинами. Припустима затримка пов'язана з тим, що несвоєчасна інформація може втратити практичну цінність, а, отже, мережа не забезпечує виконання заданих функцій. Таким чином, повинна виконуватися умова: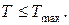

5 Обмеження на топологію мережі. Як відзначалося, з одного боку, мережа повинна мати 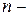связність із міркувань заданої надійності, а з іншого боку - максимальний порядок вузла, тобто число приєднаних до нього каналів не може бути більше деякої припустимої величини.