Неаналітичні методи оптимізації
Найбільш необхідні спеціальні методи аналізу, синтезу й оптимізації при побудові топологічних структур, що забезпечують необхідну надійність мережі. Для розрахунку цієї характеристики необхідно знати або мати можливість оцінювати інтенсивність відмов усіх елементів, що входять до мережі.
Детальний аналіз надійності містить у собі облік відмов елементів, вплив їх на вимоги, пов'язані з характеристиками потоків, стратегії розподілу потоків по лініях, припустимі затримки й інші істотні показники мережі. При такому аналізі робиться обчислення математичного очікування пропускних здатностей неушкоджених частин всієї мережі.
Чисто аналітичні способи аналізу незастосовні до великих мереж через великий обсяг обчислень, за винятком, може, обчислень для мереж з деревоподібною структурою. Тому при знаходженні оцінок імовірнісних параметрів широко застосовуються методи статистичного моделювання.
Розглянемо приклад завдання аналізу характеристик надійності мережі, що складається з вузлів і галузей. Імовірність виходу з ладу кожного елемента дорівнює р. Потрібно оцінити або h(p) – імовірність порушення з'єднань у мережі через ушкодження компонентів, або математичне очікування для р значень числа пара вузлів, між якими неможливо здійснити зв'язок.
Існує три способи рішення цього завдання.
Перший спосіб називається примітивним і полягає в наступному. Моделюванням для кожного елемента одержують деяке випадкове число. Якщо воно менше р, то один з елементів уважається ушкодженим і вилучається з мережі, потім мережа перевіряється на зв'язність і визначається кількість незв'язаних у цьому випадку пар вузлів. Обчислення повторюються багаторазово, що необхідно для одержання досить точної оцінки для кожного з k значень h.
Другий спосіб називається способом функціонального моделювання. У ньому, як і в примітивному способі, для кожного елемента одержують деяке випадкове число. Елементи й відповідні числа групують за парами, причому числа розміщаються у порядку убування ( 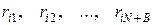 - зазначені випадкові значення,
- зазначені випадкові значення, 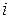 - номер елемента). Відповідно до примітивного методу, якщо
- номер елемента). Відповідно до примітивного методу, якщо 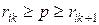 ,необхідно проаналізувати на зв'язність підсіть, яка складається з елементів
,необхідно проаналізувати на зв'язність підсіть, яка складається з елементів 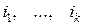 . При цьому значення зв'язності й показника надійності може бути знайдене для кожного значення р за допомогою наступної процедури: при
. При цьому значення зв'язності й показника надійності може бути знайдене для кожного значення р за допомогою наступної процедури: при 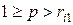 мережа не містить несправних вузлів або галузей; при
мережа не містить несправних вузлів або галузей; при 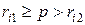 мережа складається з елементів
мережа складається з елементів 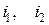 і т.д.
і т.д.
Таким способом можна скористатися для «корекції» результатів у процесі аналізу заданої мережі при введенні до неї додаткових резервних елементів. Щодо цього він ефективний і дає можливість вирішувати завдання синтезу мереж при введенні нових компонентів до структури з номером від i1 до 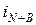 . Одночасно можна виконати аналіз підмереж, складених з
. Одночасно можна виконати аналіз підмереж, складених з 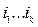 , і, для
, і, для 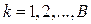 . Зокрема, можна визначити h(р) або п(р) відразу для ряду значень р, використовуючи алгоритм зв’язності один раз для кожної точки вибору.
. Зокрема, можна визначити h(р) або п(р) відразу для ряду значень р, використовуючи алгоритм зв’язності один раз для кожної точки вибору.
Третий спосіб – метод Мура-Шеннона, заснований на застосуванні наступних співвідношень для h (р) і п(р):
 , (46)
, (46)
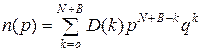 , (47)
, (47)
де 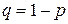 -імовірність безвідмовної роботи елемента ІМ, а
-імовірність безвідмовної роботи елемента ІМ, а 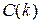 - число незв'язаних підмереж, що містять рівну кількість N елементів, і
- число незв'язаних підмереж, що містять рівну кількість N елементів, і 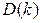 - середнє число пар вузлів, не зв'язаних між собою у всіх підмережах, що містять рівну кількість А елементів.
- середнє число пар вузлів, не зв'язаних між собою у всіх підмережах, що містять рівну кількість А елементів.
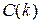 і
і 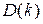 перебувають за допомогою моделювання, тому що всі
перебувають за допомогою моделювання, тому що всі 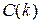 й
й 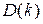 , крім
, крім 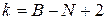 , відомі заздалегідь. Є
, відомі заздалегідь. Є 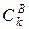 підмереж, що містять рівну кількість
підмереж, що містять рівну кількість 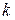 елементів. Для малих
елементів. Для малих 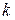
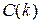 і
і 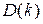 можна знайти шляхом простого перерахування.
можна знайти шляхом простого перерахування.
Дата добавления: 2021-12-14; просмотров: 451;











