Основні завдання оптимізації ІМ

Розглянемо деякі типові варіанти оптимізаційних завдань, пов'язаних з топологічним проектуванням ІМ. Можлива наступна їхня класифікація [6].

1 Вибір оптимальної пропускної здатності (ВСП).

Дано: топологія мережі, потоки, маршрути. Потрібно: мінімізувати затримки Т за змінною пропускною здатності каналів 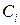при обмеженнях на вартість 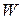і пропускні здатності :

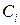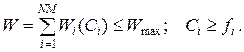
2 Розподіл потоку.

Дано: топологія мережі, потоки, пропускні здатності каналів. Потрібно: мінімізувати Т за змінною «маршрут руху» при заданих обмеженнях на потоки.

3 Оптимальний розподіл потоків і одночасно вибір пропускних здатностей.

Дано: топологія мережі, потоки. Потрібно: мінімізувати 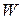за змінними «маршрут» і «пропускна здатність» ін. і заданих обмеженнях на потік і час затримки.

4 Визначення оптимальної топології мережі.

Дано: характеристики трафіка ІМ. Потрібно: мінімізувати за змінними «топологія», «маршрут» і «пропускна здатність» при обмеженнях на потік, затримку й топологію.

Розглянемо завдання оптимізації пропускних здатностей ліній. Висока пропускна здатність ліній приводить до збільшення витрат, а при малій відбуваються перевантаження й затримки повідомлень. Співвідношення між вартістю й пропускною здатністю ліній має вигляд

,

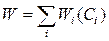де W - повна вартість ліній; Wi - вартісний коефіцієнт для i-лінії; Ci-пропускна здатність i-лінії.

Значення Wi нерівні, тому що лінії мають різні довжини. Зокрема, співвідношення між вартістю й пропускною здатністю може бути задано законом

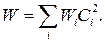
Середня затримка для 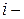й лінії задається часом очікування у черзі при допущеннях, що довжина повідомлень має експонентний розподіл:

,

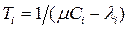де 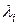— інтенсивність потоку повідомлень у 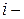м каналі; 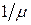— середня довжина повідомлень (у бітах).

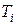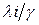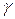Середнє значення затримки за всіма складовими виходить шляхом усереднення значення взятого з ваговими коефіцієнтами , де - сумарна швидкість надходження повідомлень. Таким чином, середня затримка Т при цьому визначається вираженням

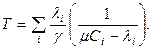(42)

Шукані пропускні здатності, які мінімізують Т при постійному W, визначаються методом невизначених множників Лагранжа. Опускаючи відповідні математичні перетворення, наведемо результат у готовому виді:

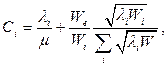(43)

де 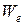— визначається вираженням

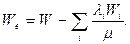
Перший доданок 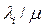, у правій частині формули для 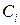- пропускна здатність лінії у режимі насичення, а другий доданок - додаткова пропускна здатність цієї лінії.

Величина результуючої транзитної затримки при передачі по лініях із пропускними здатностями 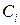вищенаведеними рівностями, що задаються (43) , визначається так:

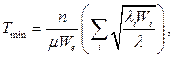(44)

де 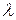- сума інтенсивностей трафіка 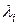по всіх лініях.

Розглянуте завдання дозволяє при заданому обмеженні на вартість каналів зв'язку так вибрати пропускні здатності, щоб середня затримка повідомлень були мінімальною.

До числа оптимізаційних завдань синтезу ІМ ставиться завдання розподілу потоків. У попереднім завданні вибирали пропускні здатності каналів при заданій конфігурації потоків. У даному завданні пропускні здатності задані, а потоки треба розподілити так, щоб мінімізувати середню затримку Т. Передбачається, що всі пропускні здатності задовольняють вимогам трафіка, а процедури вибору шляхи фіксовані й однозначні.

Як вихідне вираження для рішення завдання використаємо наведену вище формулу. У цьому випадку завдання оптимального розподілу потоків являє собою мінімізацію нелінійної функції Т за потоками 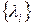при умовах виконання закону збереження потоків у кожному вузлі.

Відповідно до цього закону сумарний трафік 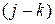, що надходить у вузол п, дорівнює сумарному трафіку 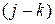, що виходить із вузла, за винятком випадків, коли вузол 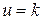; є вузлом-джерелом або при 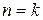- вузлом призначення. На пропускні здатності накладаються обмеження, що складаються в тім, що потік 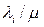у каналі 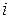не має бути негативним й меншим пропускної здатності, тобто .

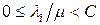Виявляється, що при цих умовах і обмеженнях Т є опукла функція потоків, а безліч реалізованих потоків зображується математичною моделлю у вигляді опуклого багатогранника в 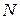-мірному просторі параметрів потоків. Розглянуте завдання вирішується симплексом-методом, що згадувався вище. Якщо вона має реалізоване рішення, то будь-який локальний мінімум є глобальним мінімумом для Т.

Часто при оптимізації ІМ використається метод відхилення потоку (ОП), суть якого полягає в знаходженні вартості мережі для значень «довжин» 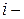х ребер. Значення довжин ребер задаються вираженням

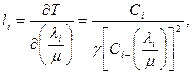(45)

при цьому потік у каналі дорівнює 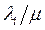. Такі «довжини» або «вартісні коефіцієнти», що відповідають їм, використають для формулювання завдання відшукання потоків по найкоротшими шляхами і з'ясування питання про те, яка частина вихідного потоку має бути відхилена. Процес рішення циклічно повторюється доти, поки не будуть отримані прийнятні значення 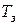. Оптимальний алгоритм ОП дає мінімальне значення Т - середню затримку повідомлення в мережі.

Методи оптимізації