Визначення теперішньої вартості грошей у фінансових розрахунках

Однією із форм визначення часової вартості грошових пото­ків на противагу компаундуванню є дисконтування (англ. — discounting).

Дисконтування є фінансово-математичною моделлю визначен­ня поточної (теперішньої) вартості грошових потоків, надхо­дження яких, як очікується, матиме місце у майбутньому протя­гом певного планового періоду. Теперішня вартість майбутніх гро­шових потоків визначається шляхом приведення — дисконтування на величину процента, який міг-би бути заробленим у випадку, коли б грошові кошти були доступні для їх використання на момент оцінювання. Отже, теперішня вартість майбутнього грошового по­току дорівнює абсолютній величині грошових коштів, інвестування якої на прийнятих для дисконтування умовах через визначений проміжок часу дало б вартість, еквівалентну вартості майбутнього грошового потоку, що аналізується. Такий підхід дає можливість фінансовому менеджеру, так само, як і у разі компаундування, отримати зіставні абсолютні величини вартості грошей для при­йняття адекватних управлінських рішень щодо інвестування.

Практичне застосування дисконтування для визначення при­веденої теперішньої вартості грошових потоків вимагає відповід­ної фінансово-математичної формалізації моделі дисконтування

визначення абсолютної величини дисконту. Залежно від по­треб аналізу грошових потоків та зміни їх вартості у часі можуть використовуватися такі моделі дисконтування:

просте дисконтування;

дисконтування ануїтетів (відстроченої або авансової ренти).

Під простіш дисконтуванням (single discounting) розуміється фінансово-математична модель розрахунку приведеної вартості майбутнього грошового потоку, отримання якого, як очікується, відбудеться одноразово через чітко визначений період. Результа­том простого дисконтування є приведена теперішня вартість (present value або PV) окремого майбутнього грошового потоку.

Процеси компаундування і дисконтування тісно взаємо­зв’язані один з одним. Визначення поточної вартості (дисконту­вання) є прямою протилежністю компаундуванню. Таким чином, якщо нам відомий показник майбутньої вартості грошей (FV), то за допомогою дисконтування ми можемо розрахувати їх тепері­шню вартість (РУ).

Оскільки оцінка майбутньої вартості грошових потоків із ви­користанням простого процента відповідає формулі (4.2)

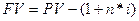
то дисконтування майбутніх грошових потоків із використанням простого процента відповідає такій формулі:

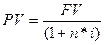
де РV — приведена теперішня вартість мабутнього грошового потоку;

FV— абсолютна величина майбутнього грошового потоку; n — кількість інтервалів у плановому періоді; і — ставка дисконтування (виражена десятковим дробом).

Оскільки майбутня вартість наявних грошових коштів у разі ви­користання складного процента визначається за формулою (4.3):

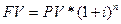
то приведена теперішня вартість майбутніх грошових потоків при використанні складного процента визначається за такою фо­рмулою:

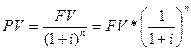
Можна визначити теперішню вартість майбутнього грошового потоку із використанням фінансової таблиці А-3, яка містить аб­солютне значення ставки дисконтування, виходячи із рівня про­центної ставки та кількості інтервалів у плановому періоді.

Частина рівняння (4.13), взята в дужки, називається фактором процента поточної вартості PVIF.

Таким чином, якщо

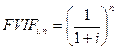
то формула (4.13) матиме вигляд:

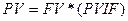
Де PVIFi,n— абсолютне значення ставки дисконтування;

і — процентна ставка;

n — кількість інтервалів у плановому періоді.

Приклад 4 6

Яку суму грошей повинен покласти підприємепь V банк на депозитний рахунок V поточний підприємець у банк на депозитний рахунок у поточний момент часу, якщо за процентної ставки 5 % за умови нарахуван­ня складного процента через п’ять років він планує отримати 127,63 Тр. од.?

Розв ’язок

Як бачимо, приклад 4.6 і приклад 4.2 мають дещо спільне: процентна ставка і термін, на який кладуться гроші на депо­зит,— однакові. Проте в прикладі 4.2 визначена сума, яку під­приємець має покласти на депозит, є заданою, а в прикладі 4.6 ми повинні визначити цю суму. У прикладі 4.6 задається очікувана сума через п’ять років, а в прикладі 4.2, навпаки, саме ця сума невідома. Отже, приклад 4.6 є оберненим до прикладу 4.2.

Застосовуючи формули (4.13), (4.14) та дані таблиці А-3, ви­значимо суму, яку необхідно покласти на депозит сьогодні:

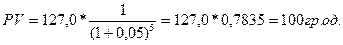
Дисконтування грошових потоків застосовується також за не­обхідності оцінювання поточної вартості цінних паперів, об’єктів нерухомості, що плануються до продажу у майбутньому.

Приклад 4.7.

Підприємець має цінний папір, який надає йому право на отримання після двох років 1000 гр. од. Річна вартість грошей на ринку капіталу сьогодні становить 16 %. Скільки коштує цей цінний папір сьогодні?

Розв язок

Застосовуючи формули (4.13), (4.14) та дані таблиці А-3, має­мо вартість цінного папера на сьогодні:

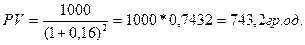
Різноплановість руху грошових коштів у результаті підприєм­ницької діяльності створює ситуацію, коли застосування просто­го дисконтування для оцінки приведеної вартості майбутніх гро­шових потоків є недостатнім. Передусім це стосується оцінки грошових потоків, які виникають протягом усього періоду із пев- ною періодичністю, тобто ануїтетів (ренти).

Якщо припустити, що абсолютна величина грошових потоків протягом періоду, який аналізується, однакова і постійна, тобто умови ануїтету передбачають рівність окремих грошових пото­ків, формула теперішньої вартості ануїтету матиме вигляд

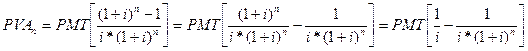
де PVA —теперішня вартість ануїтету;

PMT— абсолютна величина періодичних рівновеликих ви­плат (ануїтетів);

n — кількість інтервалів у плановому періоді; і — ставка дисконтування (виражена десятковим дробом).

Різниця в дужках рівняння (4.15) називається фактором про­цента поточної вартості ануїтетів (PVIFA). Фактор процента поточної вартості ренти — це показник ануїтетів за n-ну кількість періодів, дисконтований на і процента. У фінансових таблицях А-4 обчислено значення цього показника для різних n та і.

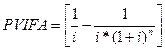
Тоді рівняння (4.15) матиме вигляд:

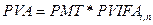
Фінансово-математична модель визначення теперішньої вар­тості ануїтетів застосовується для обчислення постійних рівних виплат з погашення кредиту, орендних платежів за користування активами підприємства, для порівняння теперішньої вартості цінних паперів, які дисконтуються під різні процентні ставки та приносять власникові певний щорічний дохід, для визначення суми, яку необхідно покласти на депозит за умови вилучення з рахунка кожного року однакової суми грошей.

Приклад 4.8.

Яку суму підприємець має покласти на депозит СЬОгодні під 10% річних, щоб протягом п’яти років щорічно знімати з рахунка по 300 гр. од.?

Розв язок

Ідеться про дисконтування ануїтетів на суму 300 гр. од. протя­гом п’яти років. Скористаємося формулою визначення теперіш­ньої вартості ануїтетів (4.15), (4.16) та даними таблиці А-4.

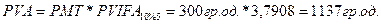
За результатами застосування табличного способу вирішення задачі маємо, що вклад у розмірі 1137 гр. од. дає змогу інвестору протягом п’яти років у кінці кожного року знімати з рахунка по 300 гр. од. за умови нарахування банком складного процента у розмірі 10 % річних. Перевіримо правильність отриманого резуль­тату арифметично, звівши розрахунки у табл. 4.5

Таблиця 4.5