Розрахунок поточної вартості звичайного ануїтету, гр. од.
| Рік | Залишок на початок року | Нарахований процент (Гр. 2x10 %) | Залишок на кінець року без щорічних вирахувань (Гр. 2 + Гр. 3) | Щорічне вилучення з рахунка | Залишок на кінець року (Гр. 4 - Гр. 5) |
| Гр. 1 | Гр. 2 | Гр.З | Гр. 4 | Гр. 5 | Гр. 6 |
| 1137,0 | 114,0 | 125,1 | 300,0 | 951,0 | |
| 951,0 | 95,1 | 1046,1 | 300,0 | 746,1 | |
| 746,1 | 74,6 | 820,7 | 300,0 | 520,7 | |
| 520,7 | 52,0 | 572,7 | 300,0 | 272,7 | |
| 272,7 | 27,3 | 300,0 | 300,0 | ||
| Усього | X | 363,0 | X | 1500,0 | X |
Різниця між початковим вкладом та знятою з рахунка сумою (сумою накопичення) є сумою процентів, що нараховуються на залишок вкладу:
1500- 1137 = 363,0 гр. од.
У прикладі 4.8 ануїтет виникав наприкінці кожного року (по- стнумерандо). Отже, формула (4.15) стосується звичайного (відстроченого) ануїтету (ренти). Проте, якщо має місце авансова рента, порядок розрахунку теперішньої вартості грошового потоку дещо змінюється. Необхідність коригування відстроченої ренти обумовлена відмінностями у порядку руху грошових коштів. Для звичайного ануїтету грошові потоки, вартість яких оцінюється, виникають по закінченні першого інтервалу аналізованого періоду (тому звичайний ануїтет називають також відстроченим). Для авансового ануїтету характерним є рух грошових коштів уже на початку першого інтервалу планового періоду. Згадані особливості обумовлюють відмінність між відстроченим та авансовим ануїтетом на один інтервал, що і відображає формула оцінки приведеної вартості авансового ануїтету:
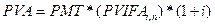
За авансового ануїтету кожний період дисконтується однією виплатою. Оскільки виплати виконуються швидше, така рента має більшу вартість, ніж звичайна. Значення авансової ренти може бути розраховано множенням показника РУ звичайної ренти на (1 + і).
Приклад 4.9.
Щорічні відрахування становлять 300 гр. од. протягом п’яти років. Ставка дисконту становить 10 %. Визначити теперішню вартість ренти за умови виникнення ануїтетів на початку кожного року.
Розв ’язок
Застосовуючи формулу (4.17) та значення таблиці А-4, отримаємо результат: .
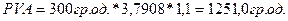
У розділі розглянуто основні фінансово-математичні моделі, які можуть бути застосовані для оцінювання прибутковості різноманітних інвестиційних проектів та вибору з них оптимальнішого.
Проте, застосовуючи математичний апарат для обрання того чи іншого варіанта вкладання грошових коштів, фінансовий менеджер повинен також зважати на обставини суб’єктивного характеру, які неможливо формалізувати в ту чи іншу фінансово- математичну модель: джерела виникнення початкового капіталу; репутація фірми, у справу якої інвестуються кошти; економічна та політична стабільність у країні та ін.
Питання для самоконтролю
Назвіть основні причини зміни вартості грошей у часі.
У чому полягає необхідність та сутність визначення вартості грошей у часі?
Назвіть випадки, в яких фінансовий менеджер повинен враховувати особливості впливу ефекту зміни вартості грошей у часі на фінансові процеси?
Що є об’єктом кількісної оцінки вартості грошей у часі?
Що є методологічною основою визначення вартості грошей у часі?
Назвіть види процентів та методи їх розрахунку. Дайте визначення простого та складного процента. Яка між ними різниця?
Дайте визначення процесам компаундування та дисконтування. Яким є зв’язок між вартістю грошей у теперішній і майбутній час?
Яка формула використовується для розрахунку суми простого процента в процесі прирощення вартості?
Яка формула використовується для розрахунку майбутньої суми вкладу (вартості грошей) у процесі його прирощення за простими процентами?
Що є коефіцієнтом нарощення суми простих процентів?
Яка формула використовується для розрахунку майбутньої суми вкладу (вартості грошей) у процесі його прирощення за складними процентами?
Яким чином коригується процентна ставка та кількість періодів нарахування процентів при нарахуванні відсотків, здійснюваному частіше за один раз на рік?
Перелічіть типи завдань щодо визначення зміни вартості грошей у часі.
Які ви знаєте способи вирішення завдань щодо визначення зміни вартості грошей у часі?
Дайте визначення компаундуванню як одному з механізмів оцінювання часової вартості грошових потоків.
У чому сутність простого компаундування?
Дайте визначення ануїтету (ренти). У яких випадках визначення майбутньої вартості грошових потоків застосовується компаундування ануїтетів (ренти)?
У чому різниця між звичайним та авансовим ануїтетом?
Який вигляд мають фінансово-математичні моделі простого компаундування, оцінки майбутньої вартості звичайного та авансового ануїтетів?
Дайте визначення дисконтуванню як одному з механізмів оцінювання часової вартості грошових потоків.
У чому сутність простого дисконтування?
У яких випадках застосування механізму простого дисконтування є недостатнім для оцінювання приведеної вартості майбутніх грошових потоків? У чому полягає сутність дисконтування ануїтетів?
Який вигляд ма;оть фінансово-математичні моделі простого дисконтування, дисконтування звичайного та авансового ануїтетів?
Чим обумовлена необхідність коригування фінансово-математичної моделі оцінювання відстроченої ренти під час оцінювання авансової ренти?
Які обставини суб’єктивного характеру повинен ураховувати фінансовий менеджер, застосовуючи математичний апарат визначення вартості грошей у часі для обрання того чи іншого варіанта вкладання грошових коштів?
Дата добавления: 2021-12-14; просмотров: 511;











