Розрахунок майбутньої вартості звичайного ануїтету, гр. од.
| Рік | Сума вкладу на початок року | Сума приросту вкладу (гр. 2 *5 %) | Сума вкладу на кінець року (гр. 2 + гр. 3 + 100 гр. од.) |
| Гр. 1 | Гр. 2 | Гр. 3 | Гр. 4 |
| 100,0 | |||
| 100,0 | 5,00 | 205,0 | |
| 205,0 | 10,25 | 315,25 | |
| 315,25 | 15,76 | 431,01 | |
| 431,01 | 21,55 | 552,56 | |
| Усього | X | 52,56 | X |
Ураховуючи, що умови ануїтету передбачають рівність та рівномірність окремих грошових потоків РМТ (у нашому випадку сума вкладів), фінансово-математична модель оцінки майбутньої вартості ануїтету може бути відображена у такий спосіб:
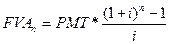
де FVA — майбутня вартість ануїтету;
РМТ — абсолютна величина періодичних рівновеликих виплат (ануїтетів);
n — кількість інтервалів у плановому періоді;
і — процентна ставка (виражена десятковим дробом);
Визначення майбутньої вартості ануїтетів за допомогою таблиць передбачає використання фактору процента майбутньої вартості ануїтетів (FVFIA) за п періодів з /-процентною ставкою.
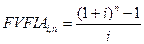
Значення FVFIA в таблиці Л-2 вже підраховано для різних комбінацій і та п. Для того щоб обчислити майбутню вартість ануїтетів за допомогою таблиць, використовується формула:
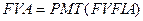
У таблиці Л-2 на перехрещенні 5 років та 5 % знаходимо значення ЕУІРА = 5,5256.
При використанні формули (4.10) визначимо майбутню вартість ануїтетів у 100 гр. од. для 5 років при 5 % ставці.
100 грн х (5,5256) = 552,56 гр. од.
Слід звернути увагу, що формула (4.10) стосується звичайного (відстроченого) ануїтету (ренти).
Проте якщо має місце авансовий ануїтет (рента), порядок кількісної оцінки майбутньої вартості грошового потоку дещо змінюється.
Приклад 4.4.
Вклади в однаковій сумі 100 гр. од. здійснюються на депозитний рахунок на початку кожного року під 5 % річних протягом п’яти років. Скільки грошей буде на рахунку наприкінці п’ятого року?
Арифметичний розв’язок задачі зведемо в таблицю (табл. 4.4).
Таблиця 4.4
Дата добавления: 2021-12-14; просмотров: 469;











