Розрахунок майбутньої вартості поточного вкладу за умови нарахування складних процентів, гр. од.
| Рік | Сума вкладу на початок року | Сума приросту вкладу (гр. 1x5 %) | Сума вкладу на кінець року (гр. 2 + гр. 3) |
| Гр. 1 | Гр. 2 | Гр. 3 | Гр. 4 |
| 5,0 | 105,0 | ||
| 105,0 | 5,25 | 110,25 | |
| 110,25 | 5,51 | 115,76 | |
| 115,76 | 5,79 | 121,55 | |
| 121,55 | 6,08 | 127,63 | |
| Усього | X | 27,63 | X |
З розрахунків, наведених у таблиці, зрозуміло, що за умови нарахування складних процентів через п’ять років підприємець матиме 127,63 гр. од.
Значно простіше можна визначити майбутню вартість теперішнього грошового потоку із використанням фінансових таблиць, які містять абсолютне значення ставки нарощення, виходячи із рівня ставки та кількості інтервалів нарахувань процентів.
У додатку до розділу наведено математичну таблицю А-1, у якій підраховано фактор майбутньої вартості процента для різноманітних комбінацій і та п (РУІРІП), тобто визначена майбутня вартість однієї грошової одиниці, залишеної на рахунку на п періодів під /-процентну ставку.
Якщо
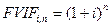
То формула матиме вигляд:
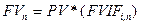
де FVIF— абсолютне значення ставки нарощення;
і — процентна ставка (виражена десятковим дробом);
n — кількість інтервалів у плановому періоді.
У нашому вииадку в таблиці А-1 РУШ для п’яти років із 5-процентною ставкою знаходимо цифру, яка стоїть на перехрещенні стошічика для періоду 5 і стовичика для 5 %. Бачимо, що РУ1Р = 1,2763.
Звшси FV= PV (FVIF)= 100 гр. од. • (1,2763) = = 127,63 гр. од.
За наявності фінансового калькулятора поступово вводимо значення N, I, PV, N. Натиснувши кнопку FV, отримаємо відповідь (ири введенні даних прикладу 4.2 отримаємо FV= 127,63).
До впровадження фінансових калькуляторів та таблиць фінансові менеджери використовували «Правило числа 72», яке дас можливість приблизно визначити, яка комбінація рівня процентної ставки і термінів вкладу приведе до подвоєння вкладеного капіталу. Наприклад, інвестиції з 9-процентним річним доходом подвоюються приблизно за вісім років (8 ■ 9 = 72). Інвестиція з доходом 6 % на рік вимагає 12 років для подвоєння вкладеного капіталу, і так далі. Використавши фінансові таблиці або фінансовий калькулятор, легко переконатися в дієвості цього правила.
У попередніх прикладах ми оперували поняттями «одноразовий внесок», «вклад». Різноплановість руху грошових потоків у результаті підприємницької діяльності створює ситуацію, коли застосування простого нарощення для кількісної оцінки майбутньої вартості грошових ресурсів недостатньо. Це стосується оцінки грошових потоків, які виникають протягом усього періоду з певною періодичністю.
Ануїтет (annuity) (рента) — це серія рівновеликих платежів (внесків) протягом визначеної кількості періодів. Розрізняють звичайний та авансовий ануїтет.
За звичайного ануїтету платежі здійснюються наприкінці кожного періоду (постнумерандо), за авансового — на початку кожного періоду (пренумерандо).
Ануїтет може бути вихідним грошовим потоком підприємця (здійснення періодичних рівновеликих внесків на рахунок банківської установи) або вхідним грошовим потоком (надходження орендної плати, яка найчастіше встановлюється однаковою фіксованою сумою)/
Приклад 4.3.
Вклади в однаковій сумі 100 гр. од. здійснюються на депозитний рахунок наприкінці кожного року під 5 % річних протягом п’яти років. Скільки грошей буде на рахунку наприкінці п’ятого року?
Арифметичне рішення прикладу зведемо в табл. 4.3.
Таблиця 4.3
Дата добавления: 2021-12-14; просмотров: 516;











