Рассмотреть только случай, когда проективная система координат задана классом эквивалентности базисов.

Решение.

Рис. 5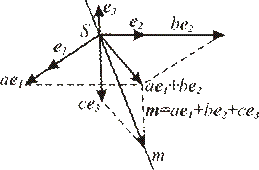

4. На проективной плоскости в модели пополненной плоскости построить точку с координатами (a:b:c) относительно проективной системы координат R={E1,E2,E3,E} .

Рассмотреть случаи, когда

а) все базисные точки E1,E2,E3,E являются собственными точками плоскости,

б) одна из четырех базисных точек E1,E2,E3,E является бесконечно удаленной точкой плоскости,

в) две из четырех базисных точек E1,E2,E3,E являются бесконечно удаленными точками плоскости.

Решение.

Рис. 6

Рис. 7

Обратить внимание на то, что параллельные прямые на пополненной плоскости имеют общую бесконечно удаленную точку.

5. Даны две проективные системы координат R={E1,E2,E3,E} и R’={E’1,E’2,E’3,E’}, причем точки E’1,E’2,E’3,E’ имеют относительно R координаты 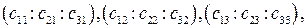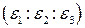соответственно. Обозначим координаты некоторой точки M 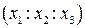относительно R и 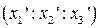относительно R’. По координатам относительно R уметь находить координаты относительно R’ и обратно.

Решение

Запишем формулы преобразования координат точек и подставим в них координаты точки М.

1) Проверим, согласованы или нет координаты точек системы R’.

Это означает следующее. Точки E’1,E’2,E’3,E’ порождаются векторами e’1, e’2,e’3,e’ с координатами 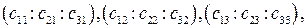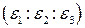. При этом, возможно, что e’1+e’2+e’3 = e’ или e’1+e’2+e’3 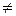e’. В первом случае координаты точек E’1,E’2,E’3,E’ называются согласованными, а во втором случае – несогласованными. Итак, проверим выполнение равенств

.

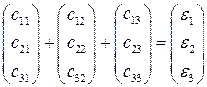Если равенство выполняется, то есть координаты точек согласованы, то переходим к действию 2).

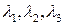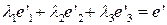Если равенство не выполняется, то есть координаты точек не согласованы, то согласуем их. Для этого найдем такие числа , что . Числа 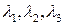находятся из системы линейных уравнений

.

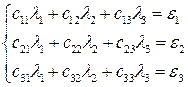Векторы 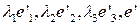теперь согласованы. Переобозначим их опять через e’1, e’2,e’3,e’.

2) Так как координаты точек E’1,E’2,E’3,E’ согласованы, то можно считать, что базис e’1, e’2,e’3 являются одним из базисов, порождающих проективную систему координат R.

Рассмотрим вектор m, порождающий точку М. Он имеет координаты 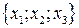относительно базиса e1, e2,e3 и 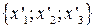относительно базиса e’1, e’2,e’3. По формулам преобразования координат векторов

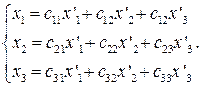
Проективные координаты точек определяются с точностью до пропорциональности. Поэтому пишут

.

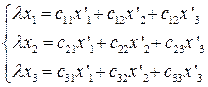Это формулы преобразования координат точек на проективной плоскости.

Если нам даны координаты 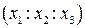точки М относительно R, то подставив их, решим систему уравнений относительно 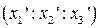. Мы найдем координаты точки М относительно R’.

Если нам даны координаты 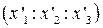точки М относительно R’, то подставив их, решим систему уравнений относительно 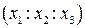. Мы найдем координаты точки М относительно R.

Тема 3. Проективные координаты точек, проективные системы координат.Второе занятие.

Список необходимых сведений. Общее уравнение прямой на плоскости. Уравнения прямой на проективной плоскости. Однородные координаты точек на пополненной плоскости и на пополненной прямой.