Практические задания

1. На проективной прямой в модели пучка прямых построить прямую пучка (проективную точку) с координатами (a:b).

Рассмотреть 2 случая:

а) проективная система координат задана классом эквивалентности базисов e1,e2 ,

б) проективная система координат задана упорядоченной тройкой прямых пучка R={e1,e2,e} .

Решение.

На рисунке 1 показано построение прямой пучка в случае а), а на рисунке 2 – в случае б). Словесное описание построения восстановите сами.

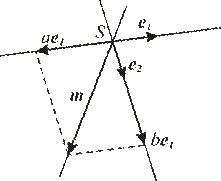
Рис.1 Рис. 2

2. На проективной прямой в модели пополненной прямой построить точку с координатами (a:b) относительно проективной системы координат R={E1,E2,E} .

Рассмотреть случай, когда все точки E1,E2,E являются обычными точками пополненной прямой, и все3 случая, когда одна из трех базисных точек E1,E2,E является бесконечно удаленной точкой.

Решение.

На рисунке 3 показано построение точки М в случае, когда точки E1,E2,E являются обычными точками пополненной прямой.

Рис.3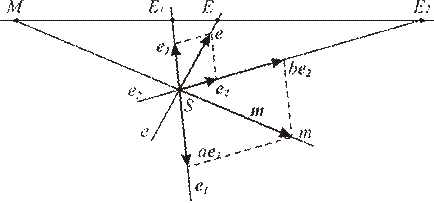

На рисунке 3 показано построение точки М в случае, когда точка E является бесконечно удаленной точкой.

Рис.4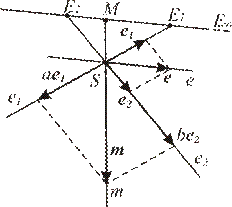

3. На проективной плоскости в модели связки прямых построить прямую пучка (проективную точку) с координатами (a:b:c).