Какие однородные координаты имеет бесконечно удаленная точка этой прямой?

Решение.

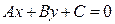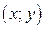Общее уравнение прямой имеет вид , где - координаты точек плоскости относительно аффинной системы координат Oe1e2.

Пополним плоскость несобственными точками и на пополненной плоскости рассмотрим проективную однородную систему координат R={E1,E2,E3,E}, где O = E3 , а точки E1, E2 порождаются векторамиe1 , e2 . При этом прямая пополнится ровно одной несобственной точкой с однородными координатами 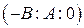, остальные точки прямой будут иметь координаты .

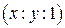Формулы связи между аффинными и проективными однородными координатами 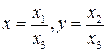. Подставим 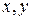в общее уравнение прямой: .

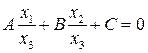Умножив уравнение на 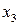, получим 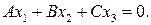Это уравнение пополненной прямой.

4. На плоскости относительно аффинной системы координат Oe1e2 написать общее уравнение прямой, если дано уравнение этой прямой в однородных координатах относительно проективной системы координат R={E1,E2,E3,E}, где O = E3 , а точки E1, E2 порождаются векторами e1 , e2 .

Решение

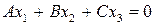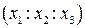Общее уравнение прямой на пополненной плоскости имеет вид , где - координаты точек относительно проективной системы координат R={E1,E2,E3,E}, E1,E2 - несобственные точки пополненной плоскости. Рассмотрим аффинную систему координат Oe1e2, где O = E3 , а точки E1, E2 порождаются векторамиe1 , e2.

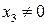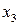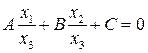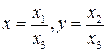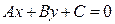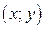На конечной части плоскости . Разделим общее уравнение на : . Формулы связи между аффинными и проективными однородными координатами . Получим , где - координаты точек плоскости относительно аффинной системы координат Oe1e2.