Практические задания

Написать уравнение бесконечно удаленной прямой в однородных координатах. Рассмотрите разные системы однородных координат на пополненной плоскости.

Решение.

Пусть проективная однородная система координат на пополненной плоскости задана так: R={E1,E2,E3,E}, где E1,E2 - несобственные точки пополненной плоскости.

Тогда несобственная прямая имеет уравнение .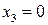

В самом деле, несобственные точки плоскости и только они порождаются векторами с координатами 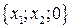относительно базиса

e1 , e2, e3 , причем векторы ei порождают точки Ei , а вектор e1 +e2 +e3 - точку E. Следовательно, несобственные точки имеют координаты .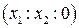

Задание. Пусть проективная однородная система координат на пополненной плоскости задана так: R={E1,E2,E3,E}, где E2,E3 или E1,E -- несобственные точки пополненной плоскости. Какое уравнение будет иметь несобственная прямая?

Решение задач на формулы связи аффинных и однородных проективных координат точек. Уметь находить однородные координаты точек по их аффинным координатам и, наоборот, по аффинным координатам проективные координаты на прямой.

Решение.

Пусть на пополненной плоскости даны аффинная система координат Oe1e2 и проективная однородная система координат R={E1,E2,E3,E}, где O = E3 , а точки E1, E2 порождаются векторамиe1 , e2 . Формулы связи между аффинными и проективными однородными координатами .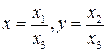

1) Рассмотрим точку с аффинными координатами 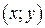и найдем ее однородные координаты 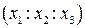. Если точка имеет аффинные координаты, то она не является несобственной. Следовательно, .

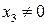Так как проективные координаты определяются с точностью до пропорциональности, то .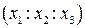

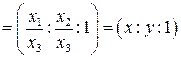2) Рассмотрим точку с однородными координатами 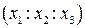и найдем ее аффинные координаты .

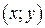Если 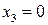, то точка является несобственной и не имеет аффинных координат.

Если 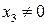, то аффинные координаты 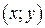точки находятся по формулам связи .

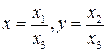3. На плоскости относительно аффинной системы координат Oe1e2 дано общее уравнение прямой. Написать уравнение этой прямой в однородных координатах относительно проективной системы координат R={E1,E2,E3,E}, где O = E3 , а точки E1, E2 порождаются векторами e1 , e2 .