Возникновение проективной геометрии. Центральное проектирование
К первой половине девятнадцатого века проективная геометрия сформировалась как самостоятельная дисциплина, объектом изучения которой стали свойства фигур и связанных с ними величин, инвариантные (не изменяющиеся) относительно того или иного проектирования. Исторически понятие проективной плоскости было создано для того, чтобы избавиться от необходимости различать случаи параллельных и пересекающихся прямых.
Становление и развитие проективной геометрии связано с именами Понселе (1788-1867), Шаля (1793-1880), Штейнера (1769-1863), Штаудта (1798-1867).
К концу девятнадцатого столетия стало ясно, что в рамках проективной геометрии создана глубокая и содержательная теория, включающая в единую схему геометрии Евклида, Лобачевского и Римана.
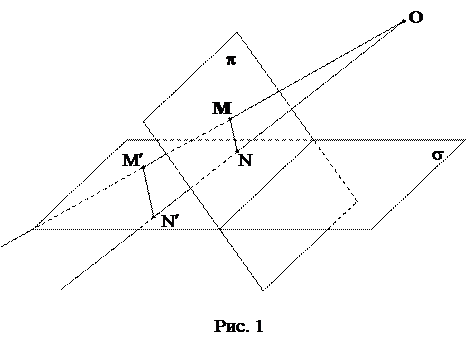 |
В действительном трехмерном евклидовом пространстве рассмотрим две плоскости
 и
и  , а также точку О, не лежащую на этих плоскостях (рисунок 1). Произвольной точке М из первой плоскости сопоставим точку M¢ пересечения прямой ОМ с плоскостью
, а также точку О, не лежащую на этих плоскостях (рисунок 1). Произвольной точке М из первой плоскости сопоставим точку M¢ пересечения прямой ОМ с плоскостью  , M¢ - проекция точки М на плоскость
, M¢ - проекция точки М на плоскость 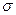 из центра О. Установленное таким образом соответствие между точками двух плоскостей называется центральным проектированием.
из центра О. Установленное таким образом соответствие между точками двух плоскостей называется центральным проектированием.
Перемещая центр проектирования в пространстве, и, изменяя положение плоскости 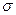 для одной и той же фигуры на неподвижной плоскости
для одной и той же фигуры на неподвижной плоскости 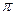 , получаем различные проекции, при этом многие свойства исходной фигуры изменяются. Так, например, не сохраняются длины отрезков, а также величины углов, нарушается, вообще говоря, параллельность прямых. Проектируя окружность, можно получить эллипс, параболу или гиперболу. Однако, проекции трех точек, лежащих на прямой, также принадлежат одной прямой (но свойство точки лежать между двумя другими не является проективным), проекцией линии второго порядка является линия второго порядка.
, получаем различные проекции, при этом многие свойства исходной фигуры изменяются. Так, например, не сохраняются длины отрезков, а также величины углов, нарушается, вообще говоря, параллельность прямых. Проектируя окружность, можно получить эллипс, параболу или гиперболу. Однако, проекции трех точек, лежащих на прямой, также принадлежат одной прямой (но свойство точки лежать между двумя другими не является проективным), проекцией линии второго порядка является линия второго порядка.
Задача 1. Докажите, что при центральном проектировании между двумя пересекающимися плоскостями трехмерного евклидова (аффинного) пространства устанавливается не взаимно однозначное соответствие.
§2. Понятие проективного пространства. Простейшие свойства
Следующее определение проективного пространства принадлежит немецкому математику Герману Вейлю (1885-1955).
Определение. Пусть Vn+1 – векторное пространство n+1 измерений над полем R действительных чисел, а V* – множество всех ненулевых векторов этого пространства, V* = Vn+1\{0}. Непустое множество Pn – называется проективным пространством n измерений (порожденным векторным пространством Vn+1), если задано отображение f : V* 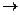 Pn, удовлетворяющее следующим условиям (аксиомам проективного пространства):
Pn, удовлетворяющее следующим условиям (аксиомам проективного пространства):
1. Отображение f – сюръективно, (т.е. любой элемент из Pn имеет хотя бы один прообраз).
2. Равенство f(x) = f(y) выполняется тогда и только тогда, когда векторы x и y коллинеарны.
Элементы множества Pn называются точками проективного пространства и обозначаются прописными буквами латинского алфавита: A, B, C, …,X, Y, … . Если f(x) =X, то говорят, что вектор x порождает точку X. Из аксиомы 2 следует, что множество всех векторов пространства V*, порождающих одну точку, есть одномерное векторное подпространство без нулевого вектора.
Так как неколлинеарные векторы порождают различные точки, то действительное проективное пространство n измерений содержит бесконечное множество точек.
Замечание. Вместо поля R можно взять любое другое поле К. Можно показать, что если поле К конечно, то полученное n-мерное проективное пространство Pn(K) будет состоять лишь из конечного множества точек. Кроме того, если поле заменить телом, или даже просто кольцом, то можно построить содержательную и интересную теорию.
В дальнейшем мы будем изучать в основном свойства действительного проективного пространства двух и трех измерений.
Пусть P3 – проективное пространство трех измерений, а V4 – четырехмерное векторное пространство над полем действительных чисел, которое порождает проективное пространство P3. Рассмотрим векторное подпространство Lk k измерений пространства V4, где k = 2, 3. Множество всех точек из P3, которые порождаются ненулевыми векторами подпространства Lk, называется прямой, если k = 2, и плоскостью, если k = 3. Говорят, что подпространство Lk порождает прямую (плоскость). Прямые будем обозначать малыми буквами латинского алфавита: a, b, c,…, а плоскости – малыми буквами греческого алфавита: 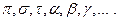
Так как подпространство Lk содержит бесконечное множество попарно неколлинеарных векторов, а неколлинеарные векторы порождают различные точки, то каждые действительные проективные прямая и плоскость являются бесконечными множествами точек.
Нетрудно доказать, что в трехмерном проективном пространстве существуют тройки точек, не лежащие на одной прямой, и четверки точек, не лежащие в одной плоскости.
В самом деле, пусть a, b, c, d – базис векторного пространства V, а A, B, C и D – точки, которые порождаются этими векторами. Тогда точки A, B, C и D не лежат в одной плоскости, а любые три из этих четырех точек не лежат на одной прямой. Докажем, например, что точки A, B и С не лежат на одной прямой. Предположим противное, то есть что эти точки лежат на некоторой прямой, порожденной двумерным векторным подпространством L2. Тогда векторы a, b и с принадлежат L2. Но это невозможно, так как эти векторы линейно независимы, и поэтому не могут быть компланарны (то есть быть параллельными одной плоскости).
Рассмотрим свойства взаимного расположения точек, прямых и плоскостей трехмерного пространства.
10. Через любые две различные точки А и В проходит одна и только одна прямая.
Пусть a и b – векторы, которые порождают точки А и В. Эти векторы не коллинеарны, так как А и В – различные точки. Рассмотрим двумерное векторное подпространство L2 (a, b) порожденное этими векторами. (Любой вектор из L2 является линейной комбинацией векторов a и b). Прямая l есть образ подпространства L2 (a, b) и, очевидно, проходит через точки А и В.
Докажем теперь, что l – единственная прямая, проходящая через точки А и В. Допустим, что l¢ – прямая, проходящая через точки A и B, а (L2)¢ – двумерное подпространство, которое порождает прямую l¢. Так как точки А и В принадлежат l¢, то векторы а и b принадлежат L¢, и поэтому L¢ – подпространство, порожденное векторами a и b. Таким образом, L¢ и L – одно и то же векторноеподпространство, и, следовательно, прямые l¢ и l совпадают.
Аналогично можно доказать следующие утверждения.
20. Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.
30. Если две различные точки А и В лежат в плоскости, то и прямая (АВ) лежит в этой плоскости (т.е. каждая точка прямой (АВ) принадлежит плоскости).
Пусть W3 – трехмерное векторное пространство, которое порождает плоскость 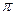 , a и b – векторы, порождающие точки А и В. При доказательстве свойства 10 мы установили, что подпространство L2 (a, b) порождает прямую (АВ). Так как A
, a и b – векторы, порождающие точки А и В. При доказательстве свойства 10 мы установили, что подпространство L2 (a, b) порождает прямую (АВ). Так как A 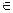
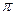 , B
, B 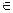
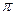 , то a
, то a 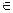 W3, b
W3, b 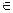 W3, поэтому L2 (a, b)
W3, поэтому L2 (a, b) 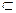 W3.
W3.
Пусть М – произвольная точка прямой (АВ), m – вектор, порождающий эту точку. Так как m 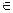 L2, то m
L2, то m 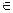 W3. Отсюда следует, что М – точка плоскости
W3. Отсюда следует, что М – точка плоскости 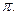
40. Любые различные две проективные прямые, лежащие в одной плоскости, пересекаются.
Пусть a и b – две прямые, лежащие в плоскости 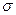 , а L, L¢ и W – векторные подпространства, которые порождают соответственно прямые a и b и плоскость
, а L, L¢ и W – векторные подпространства, которые порождают соответственно прямые a и b и плоскость 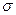 . Прямые a и b лежат в плоскости
. Прямые a и b лежат в плоскости 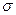 , поэтому L
, поэтому L 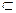 W, L¢
W, L¢ 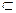 W. Так как L и L¢ – различные двумерные подпространства трехмерного векторного подпространства W, то их пересечением является одномерное векторное подпространство. Ненулевые векторы этого подпространства порождают проективную точку, которая, очевидно, является общей точкой прямых а и b.
W. Так как L и L¢ – различные двумерные подпространства трехмерного векторного подпространства W, то их пересечением является одномерное векторное подпространство. Ненулевые векторы этого подпространства порождают проективную точку, которая, очевидно, является общей точкой прямых а и b.
Две различные прямые a и b не могут иметь более чем одну общую точку, так как через две различные точки проходит только одна прямая.
Сформулируем без доказательства еще два утверждения.
50. Любая проективная плоскость и не лежащая в ней проективная прямая имеют одну и только одну общую точку.
60. Любые две различные проективные плоскости имеют общую проективную прямую, на которой лежат все общие точки этих плоскостей.
Докажем, что любую плоскость трехмерного проективного пространства можно рассматривать как двумерное проективное пространство. В самом деле, пусть 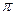 – произвольная плоскость проективного пространства P3. Обозначим через W3 трехмерное векторное подпространство пространства V4, которое порождает эту плоскость, а через W* – множество всех ненулевых векторов подпространства W3. Рассмотрим W3 как самостоятельное трехмерное векторное пространство. Так как W*
– произвольная плоскость проективного пространства P3. Обозначим через W3 трехмерное векторное подпространство пространства V4, которое порождает эту плоскость, а через W* – множество всех ненулевых векторов подпространства W3. Рассмотрим W3 как самостоятельное трехмерное векторное пространство. Так как W* 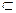 V* и
V* и 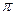
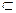 P3, то отображение f : V*
P3, то отображение f : V* 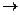 P3 порождает отображение f1 : W*
P3 порождает отображение f1 : W* 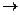
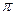 , которое каждому вектору x из W* ставит в соответствие точку f(x). Очевидно, отображение f удовлетворяет аксиомам проективного пространства. Действительно, выполнение аксиомы 1 непосредственно следует из определения плоскости, а выполнение аксиомы 2 очевидно: отображение f удовлетворяет этой аксиоме, поэтому и f1 удовлетворяет ей.
, которое каждому вектору x из W* ставит в соответствие точку f(x). Очевидно, отображение f удовлетворяет аксиомам проективного пространства. Действительно, выполнение аксиомы 1 непосредственно следует из определения плоскости, а выполнение аксиомы 2 очевидно: отображение f удовлетворяет этой аксиоме, поэтому и f1 удовлетворяет ей.
Аналогично можно доказать, что любую прямую проективного пространства двух (трех) измерений можно рассматривать как одномерное проективное пространство.
Задача 2. Пусть Z2 – поле вычетов по модулю 2. Доказать, что проективная прямая P1 над Z2 содержит точно три различные точки.
Задача 3. Доказать, что проективная плоскость P2 над Z2 содержит ровно семь различных точек и ровно семь различных прямых.
Задача 4. Доказать, что на проективной плоскости над произвольным полем существуют четыре точки, из которых никакие три не лежат на одной прямой.
Задача 5. Сколько различных точек содержит произвольная прямая проективной плоскости P2 над полем Z3 вычетов по модулю 3?
Задача 6. Пусть Zp – поле вычетов по модулю простого числа p. Доказать, что n-мерное проективное пространство Pn(Zp) состоит из 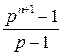 точек.
точек.
Задача 7. Сколько точек содержит произвольная прямая n-мерного проективного пространства Pn над полем Zp вычетов по модулю простого числа p?
Задача 8. Каково наименьшее число точек трехмерного проективного пространства P3 над произвольным полем?
§3. Модели проективного пространства
Рассмотрим математические примеры, подтверждающие корректность определения проективного пространства.
Говорят, что модель проективного пространства Pn обозначена, если Pn задано как множество и построено отображение f : (Vn+1\{0}) 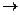 Pn, удовлетворяющее условиям 1 и 2 определения Г. Вейля.
Pn, удовлетворяющее условиям 1 и 2 определения Г. Вейля.
Проективную геометрию можно изучать в любой из ее реализаций.
1. Рассмотрим арифметическую проективную плоскость. Введем однородные координаты. В действительном векторном пространстве V3 выберем базис e1, e2, e3, тогда любой вектор m 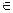 V3 однозначно раскладывается по базису m1e1+m2e2+m3e3. Можно рассмотреть арифметическое векторное пространство всех упорядоченных троек действительных чисел {[m1, m2, m3]}, которое также будем обозначать V3. Во множестве P2 точкой считаем упорядоченную тройку действительных чисел с точностью до ненулевого множителя. Например, (2,–1, 7) = (–4, 2,
V3 однозначно раскладывается по базису m1e1+m2e2+m3e3. Можно рассмотреть арифметическое векторное пространство всех упорядоченных троек действительных чисел {[m1, m2, m3]}, которое также будем обозначать V3. Во множестве P2 точкой считаем упорядоченную тройку действительных чисел с точностью до ненулевого множителя. Например, (2,–1, 7) = (–4, 2, 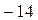 ). Построим отображение f: (V3\{0})
). Построим отображение f: (V3\{0}) 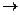 P2; [m1, m2, m3]
P2; [m1, m2, m3] 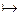 (m1, m2, m3). Условия 1 и 2 определения Г. Вейля непосредственно проверяются.
(m1, m2, m3). Условия 1 и 2 определения Г. Вейля непосредственно проверяются.
Замечание. Множество P2 является фактор множеством по отношению эквивалентности: две тройки действительных чисел эквивалентны, если одну из другой можно получить умножением на ненулевой множитель. Нулевая тройка не рассматривается.-
 |
2. Рассмотрим действительное (n+1)-мерное аффинное (евклидово) пространство, в котором фиксируем некоторую точку О. Точкой n-мерного пространства Pn будем считать прямую, проходящую через точку О. Ненулевой вектор
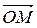 порождает единственную прямую, коллинеарную ему и проходящую через точку O.
порождает единственную прямую, коллинеарную ему и проходящую через точку O.
Аффинное пространство (n+1) измерений порождает векторное пространство Vn+1 (каждый вектор есть направленный отрезок с началом в точке О). Имеем отображение 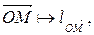 т.е. построено конкретное множество Pn и конкретное отображение
т.е. построено конкретное множество Pn и конкретное отображение
f :(Vn+1\{0}) 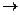 Pn.
Pn.
Для каждой прямой, проходящей через точку О, существует ненулевой вектор с началом в точке О, порождающий эту прямую. (На прямой достаточно взять точку М, отличную от точки О; вектор 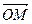 порождает эту прямую). Таким образом, f – сюръекция. Коллинеарные векторы порождают одну и ту же прямую, проходящую через точку О; обратно, любая прямая порождается коллинеарными векторами. Итак, связка прямых, проходящих через фиксированную точку (n+1)-мерного аффинного пространства, является моделью n – мерного проективного пространства.
порождает эту прямую). Таким образом, f – сюръекция. Коллинеарные векторы порождают одну и ту же прямую, проходящую через точку О; обратно, любая прямая порождается коллинеарными векторами. Итак, связка прямых, проходящих через фиксированную точку (n+1)-мерного аффинного пространства, является моделью n – мерного проективного пространства.
3. Расширенная прямая. К аффинной прямой добавим еще одну точку, которую называем бесконечно удаленной, или несобственной. Приведем более подробное разъяснение.
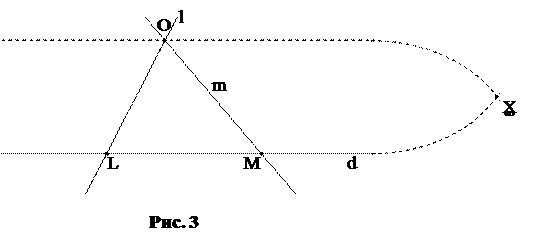 |
Вложим аффинную прямую d в аффинную плоскость. Фиксируем точку О вне прямой. Как мы уже знаем, связка прямых, проходящих через точку О, есть модель проективной прямой P1. Все прямые, проходящие через точку О, за исключением одной единственной, пересекают прямую d. Будем считать, что две параллельные в обычном смысле прямые, пересекаются в бесконечно удаленной точке 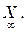 Расширенной прямой
Расширенной прямой 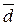 называем прямую d , пополненную несобственной точкой
называем прямую d , пополненную несобственной точкой 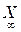 .
.
4.
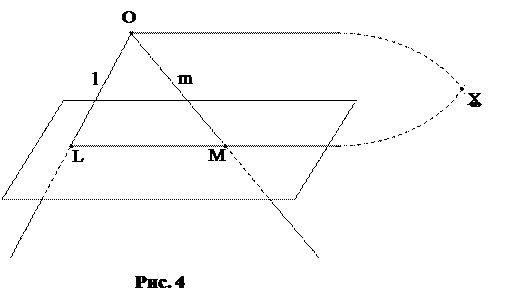 |
Расширенная плоскость. Каждую прямую аффинной плоскости пополняем несобственной точкой, так что пучок параллельных прямых пополняется одной бесконечно удаленной точкой. Если прямые не параллельны в обычном смысле, то они пополняются различными бесконечно удаленными точками. Все несобственные точки образуют несобственную прямую.
После окончания процедуры пополнения все точки и все прямые считаем равноправными.
§4. Понятие проективных координат
Пусть Vn+1 – действительное векторное пространство. Выберем базис в Vn+1: {e1, e2, …, en+1}. Произвольный вектор x из Vn+1 однозначно представляется в виде линейной комбинации базисных векторов:
x = x1e1 + x2e2 + … + xn+1en+1 = xiei, i = 1, 2, …, n+1
Допустим, что n-мерное проективное пространство Pn порождается Vn+1, т.е. задано сюръективное отображение f : (Vn+1\{0}) 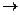 Pn, переводящее коллинеарные векторы в одну проективную точку.
Pn, переводящее коллинеарные векторы в одну проективную точку.
Определение. Говорят, что упорядоченная система (n+2) точек (A1, A2, …, An+1, E) проективного пространства Pn занимает общее положение, если никакие (n+1) точки из них не принадлежат(n-1)-мерному проективному пространству.
При n = 1: Упорядоченная система из трех точек (A1, A2, E) на проективной прямой занимает общее положение, если три точки попарно различны.
При n = 2: Упорядоченная система из четырех точек (A1, A2, A3, E) на проективной плоскости занимает общее положение, если никакие три из них не принадлежат одной прямой.
При n = 3: Упорядоченная система из пяти точек (A1, A2, A3, A4, E) в трехмерном проективном пространстве занимает общее положение, если никакие четыре из них не принадлежат одной плоскости.
Определение. Проективным репером в Pn называется упорядоченная система (n+2) точек общего положения: Â = (A1, A2, …, An+1, E). Последняя точка Е репера называется единичной.
Фиксируем некоторый проективный репер Â в Pn. Пусть векторы a1, a2, …, an+1, e из Vn+1 порождают точки A1, A2, …, An+1, E. Поскольку точки A1, A2, …, An+1 не принадлежат проективному пространству размерности n-1, то векторы a1, a2, …, an+1 образуют базис в Vn+1, а вектор e представляется в виде линейной комбинации базисных векторов:
e = e1a1+e2a2+…+en+1an+1.
Введем новые векторы bi = eiai, i = 1, 2, …, n+1. Система векторов {bi} 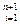 также образует базис в Vn+1 , этот базис называется согласованным с репером Â. Условие согласования имеет вид:
также образует базис в Vn+1 , этот базис называется согласованным с репером Â. Условие согласования имеет вид:
b1 + b2 + … + bn+1 = e
Произвольная точка М проективного пространства может быть порождена ненулевым вектором m = mibi. Координаты вектора m образуют проективные координаты точки M(m1, m2, m3, …, mn+1). Таким образом, каждая точка n-мерного проективного пространства имеет (n+1) координат, задаваемых с точностью до ненулевого множителя, причем все проективные координаты точки не могут одновременно обращаться в нуль.
Задача 9. На расширенной плоскости задана расширенная прямая с доступными точками проективного репера Â(A1, A2, E). Построить точки M(–1, 1), N(–4, 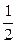 ), L(–3, 3) по их проективным координатам.
), L(–3, 3) по их проективным координатам.
Задача 10. На расширенной плоскости задана связка прямых с центром в точке О, с фиксированными прямыми a1, a2, e, образующими репер в модели проективной прямой. Построить прямые m(–1, 1), n(–4, 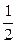 ), l(–3, 3) по их проективным координатам.
), l(–3, 3) по их проективным координатам.
Задача 11. На расширенной прямой задан проективный репер Â(A1, A2, E), причем одна из этих трех точек является бесконечно удаленной. Построить точку М по заданным ее координатам.
Задача 12. На расширенной прямой 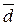 задан проективный репер Â(A1, A2, E), где A1 и A2 – собственные точки, а E – середина отрезка [A1, A2]. Найти координаты несобственной точки
задан проективный репер Â(A1, A2, E), где A1 и A2 – собственные точки, а E – середина отрезка [A1, A2]. Найти координаты несобственной точки 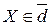 в репере Â.
в репере Â.
Задача 13. Известно, что для построения точки M(x1, x2) по ее координатам в проективном репере Â(A1, A2, E) на расширенной прямой 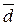 нужно выбрать на расширенной плоскости, содержащей
нужно выбрать на расширенной плоскости, содержащей 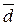 , точку O
, точку O 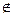
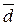 , соединить точку О с точками A1, A2, E прямыми, на единичной прямой (ОЕ) выбрать ненулевой единичный вектор е, разложить его по правилу параллелограмма на сумму базисных векторов a1 и a2, лежащих на прямых (ОA1) и (ОA2). Тогда аффинный репер (O, a1, a2) порождает проективный репер Â(A1, A2, E). По известным координатам x1 и x2 строим ненулевой вектор m = x1a1 + x2a2, m =
, соединить точку О с точками A1, A2, E прямыми, на единичной прямой (ОЕ) выбрать ненулевой единичный вектор е, разложить его по правилу параллелограмма на сумму базисных векторов a1 и a2, лежащих на прямых (ОA1) и (ОA2). Тогда аффинный репер (O, a1, a2) порождает проективный репер Â(A1, A2, E). По известным координатам x1 и x2 строим ненулевой вектор m = x1a1 + x2a2, m = 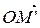 , тогда искомая точка M=(OM¢)
, тогда искомая точка M=(OM¢) 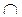
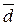 . Доказать, что положение точки М на прямой
. Доказать, что положение точки М на прямой 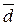 не зависит от выбора аффинного репера (O, a1, a2).
не зависит от выбора аффинного репера (O, a1, a2).
Задача 14. На расширенной прямой 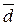 заданы собственные точки (A1, A2, E) – образующие репер Â, в котором собственная точка M
заданы собственные точки (A1, A2, E) – образующие репер Â, в котором собственная точка M 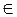
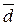 , M
, M 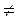 A1 имеет координаты x1, x2. Доказать:
A1 имеет координаты x1, x2. Доказать: 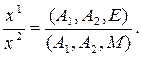
Напоминание: Если простое отношение трех точек (A1, A2, М)=t 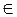 R, то это значит, что
R, то это значит, что 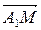 =
=  , M
, M  A1.
A1.
§5. Проективные координаты на плоскости
Критерийколлинеарности трех точек. Три точки A(a1, a2, a3), B(b1, b2, b3), C(c1, c2, c3), заданные их координатами в репере на действительной проективной плоскости, лежат на одной прямой тогда и только тогда, когда определитель, составленный из их координат, равен нулю:
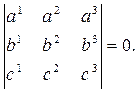
 |
Критерийколлинеарности трех точек на проективной плоскости следует из критерия компланарности трех векторов в трехмерном пространстве: три вектора компланарны (т.е. параллельны одной плоскости), если и только если определитель, составленный из их координат равен нулю.
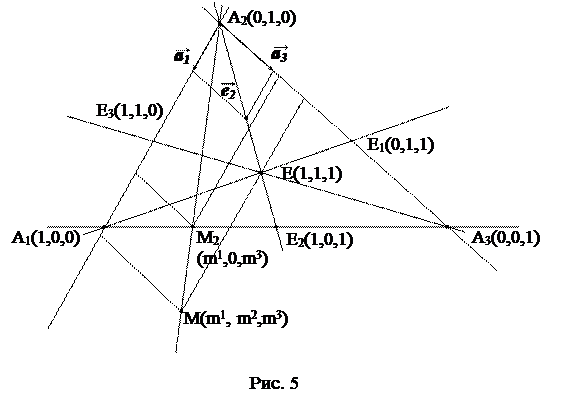
Рассмотрим подробнее репер на проективной плоскости.
Теоремао координатах проекции точки на координатную прямую.
Если произвольная точка M(m1, m2, m3), не равная A2, задана в репере Â(A1, A2, A3, E), то ее проекция M2 из точки A2 на вторую координатную прямую (A1A3) в репере Â2(A1, A2, E2) имеет координаты (m1, m3).
Доказательство. Для любой точки X(x1, x2, x3) на (A1A3) имеем согласно критерию
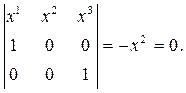
Таким образом, для точки M2 в репере Â вторая координата равна нулю. Пусть точка M2 в репере Â имеет координаты (y1, 0, y3). Применяем критерий для точек A2, M2, M, лежащих на одной прямой:
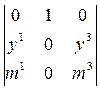 = –
= – 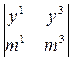 = 0. y1=pm1, y3=pm3, p
= 0. y1=pm1, y3=pm3, p  0.
0.
Без ограничения общности, можно положить р = 1. На плоскости рассмотрим, например, аффинный репер (A2, a1,a3), порождающий проективный репер Â2(A1, A3, E2) на второй координатной прямой (A1, A3).
В трехмерном аффинном пространстве существует согласованный базис a1, a2, a3, e относительно репера Â2(A1, A2, A3, E). Так как точки M2 и E2 имеют, соответственно, координаты (m1, 0, m3), (1, 0, 1) в Â, то векторы e2 = a1 + a3, m2 = m1a1 + m3a3 порождают, соответственно, точки E2 и M2.
Задача 15. На расширенной плоскости  задан проективный репер Â(A1, A2, A3, E), все четыре точки собственные. Построить следующие точки по их координатам: M(1, 2, 0), N(0, –2, –1), P(1, 2, 1), Q(0, –4, 0).
задан проективный репер Â(A1, A2, A3, E), все четыре точки собственные. Построить следующие точки по их координатам: M(1, 2, 0), N(0, –2, –1), P(1, 2, 1), Q(0, –4, 0).
Задача 16. Пусть единичная точка Е является точкой пересечения медиан (центром тяжести) координатного трехвершинника A1, A2, A3. Построить точку М(1, 1, –1) по ее координатам в проективном репере Â(A1, A2, A3, E) на расширенной плоскости  .
.
§6. Уравнение прямой на проективной плоскости
На проективной плоскости P2 выберем репер Â(A1, A2, A3, E) и две различные точки B(b1, b2, b3) и C(c1, c2, c3) с определенными координатами в заданном репере. Известно, что необходимым и достаточным условием принадлежности трех точек X(x1, x2, x3), B, C одной прямой является равенство нулю определителя, составленного из координат этих точек.
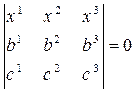 (1)
(1)
Это и есть один из способов написать уравнение прямой (ВС).
Поскольку В и С различные точки, то ранг матрицы
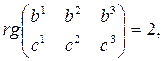 (2)
(2)
поэтому вектор-строка (x1, x2, x3) линейно выражается через векторы-строки (b1, b2, b3) и (c1, c2, c3), то есть существуют не равные одновременно нулю числа 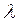 и
и 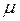 , что
, что
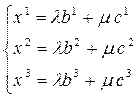 (3)
(3)
Мы получили так называемые параметрические уравнения прямой (ВС), где 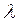 и
и 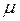 – параметры, при изменении которых меняется положение текущей точки Х на прямой (ВС).
– параметры, при изменении которых меняется положение текущей точки Х на прямой (ВС).
Теорема. Если на проективной плоскости задан репер, то установлено взаимно однозначное соответствие между классами равносильных однородных уравнений первой степени и всеми проективными прямыми.
Доказательство. Раскрыв определитель в левой части равенства (1) по первой строке, имеем
u1x1 + u2x2 + u3x3 = 0, (4)
где u1 = 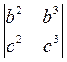 , u2 =
, u2 = 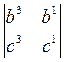 , u1 =
, u1 = 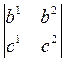 .
.
Мы действительно получили однородное уравнение первой степени, поскольку из равенства (2) следует, что все коэффициенты u1, u2, u3 одновременно не могут быть равны нулю. Координаты точек В и С задаются с точностью до ненулевого множителя, поэтому и координаты u1, u2, u3 также определяются с точностью до ненулевого множителя. Если же уравнение (4) умножить на некоторое число р, отличное от нуля, то получим
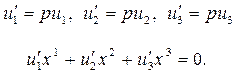 (4¢)
(4¢)
Ясно, что уравнения (4) и (4¢) равносильны.
Обратно, пусть в искомом репере Â на проективной плоскости задано уравнение (4), являющееся однородным и первой степени. Допустим, что u1 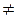 0 (Если u1=0, то отличен от нуля хотя бы один из коэффициентов u2 или u3). Точки P(–u3, 0, u1) и Q(–u2, u1, 0) имеют координаты, удовлетворяющие уравнению (4). Рассмотрим прямую (PQ):
0 (Если u1=0, то отличен от нуля хотя бы один из коэффициентов u2 или u3). Точки P(–u3, 0, u1) и Q(–u2, u1, 0) имеют координаты, удовлетворяющие уравнению (4). Рассмотрим прямую (PQ):
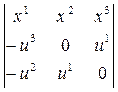 = u1(u1x1 + u2x2 + u3x3) = 0.
= u1(u1x1 + u2x2 + u3x3) = 0.
После сокращения на u1 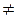 0 приходим к уравнению (4).
0 приходим к уравнению (4).
В качестве примера запишем уравнения первой координатной прямой (A2A3): x1 = 0, второй координатной прямой (A1A3): x2 = 0, третьей координатной прямой (A1A2): x3 = 0.
Определение.Коэффициенты уравнения (4) называются координатами прямой.
Т.о., прямая (A2A3) имеет координаты (1, 0, 0), (A1A3) – (0, 1, 0), (A1A2) – (0, 0, 1).
Задача 17. Построить прямую a(1, 2, –2) по ее координатам относительно заданного на расширенной плоскости проективного репера (A1, A2, A3, E).
Задача 18. Доказать, что прямые a(a1, a2, a3), b(b1, b2, b3), c(c1, c2, c3), заданные своими координатами в некотором репере на проективной плоскости, проходят через одну точку тогда и только тогда, когда определитель, составленный из их координат, равен нулю, т.е.
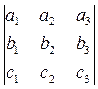 = 0
= 0
§7. Преобразование проективных координат
Пусть в n-мерном проективном пространстве Pn задано два проективных репера  = (A1, A2, …, An+1, E) и ¢ = (A¢1, A¢2, …, A¢n+1, E¢). Пусть некоторая точка М имеет координаты (x1, x2, …, xn+1) в репере  и (y1, y2, …, yn+1) в репере ¢.
Поставим задачу: найти формулы, выражающие координаты {xi}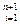 через {yi}
через {yi}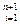 .
.
Рассмотрим координаты точек репера ¢ в репере Â:
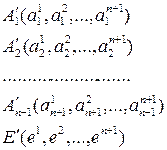
Представляя координаты точек в виде столбцов матрицы, получаем матрицу перехода A от репера  к реперу ¢, имеющую (n +2) столбца и (n+1) строку
A = 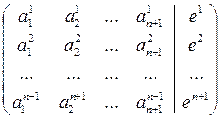 (1)
(1)
Матрица перехода от репера  к реперу ¢ называется согласованной, если сумма первых (n+1) столбцов равна последнему столбцу.
Если матрица перехода от репера  к реперу ¢ не является согласованной, то необходимо провести процедуру согласования. Для этого каждый i-ый столбец матрицы (1) умножаем на неопределенный множитель ki. (Напомним, что проективные координаты точек задаются с точностью до ненулевого множителя).
Для определения неизвестных ki, i=1,…,n+1, получаем систему линейных уравнений:
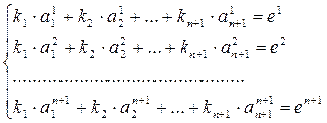 (2)
(2)
Решением системы (2) являются ненулевые множители k1, k2, …, kn+1. Заметим, что система (2) имеет нетривиальное решение, так как её главный определитель отличен от нуля. Умножая каждый столбец матрицы (1) на соответствующий множитель, получаем согласованную квадратную матрицу A¢ перехода от репера  к реперу ¢
A = (ki 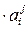 )
) 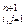 = [(a
= [(a 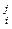 )¢]
)¢] 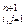
Теперь, последний столбец, составленный из координат единичной точки Е, можно не записывать.
Рассмотрим векторное пространство Vn+1, порождающее проективное пространство Pn. Пусть реперу  соответствует базис {ai}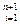 , а реперу ¢ – базис {a¢i}
, а реперу ¢ – базис {a¢i}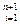 . Тогда вектор m = xjaj = x1a1 + x2a2 + … + xn+1an+1 порождает точку М. Поскольку векторы m и m¢ порождают одну и ту же точку, то они коллинеарны. Пусть, например,
. Тогда вектор m = xjaj = x1a1 + x2a2 + … + xn+1an+1 порождает точку М. Поскольку векторы m и m¢ порождают одну и ту же точку, то они коллинеарны. Пусть, например, 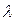 m = m¢,
m = m¢, 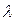
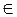 R,
R, 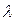
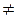 0. Векторы a¢j, j = 1, …, n+1, раскладываются по базису aj:
0. Векторы a¢j, j = 1, …, n+1, раскладываются по базису aj:
a¢j = (a 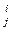 )¢ai = (a
)¢ai = (a 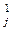 )¢a1 + (a
)¢a1 + (a 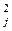 )¢a2 + … + (a
)¢a2 + … + (a 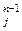 )¢an+1
)¢an+1
Итак,
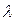 m = m¢
m = m¢ 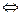
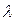 (xjaj) = yi(ai)¢ = yi(a
(xjaj) = yi(ai)¢ = yi(a 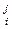 )¢aj
)¢aj
Таким образом, мы получили векторное равенство:
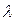 (xjaj) = [yi(a
(xjaj) = [yi(a 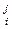 )¢]aj
)¢]aj
Поскольку {aj}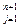 базис в Pn+1, то имеем
базис в Pn+1, то имеем 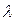 xj = yi(a
xj = yi(a 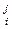 )¢, j = 1, …, n+1. Полагая для краткости(a
)¢, j = 1, …, n+1. Полагая для краткости(a 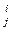 )¢ = b
)¢ = b 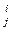 , окончательно имеем
, окончательно имеем
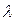 xj = b
xj = b 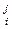 yi, j = 1, …, n+1. (3)
yi, j = 1, …, n+1. (3)
Это и есть формулы преобразования координат точки проективного простра
Дата добавления: 2021-12-14; просмотров: 956;











