Поверхности второго порядка
С ранее рассмотренными кривыми второго порядка связаны следующие поверхности. Одна из них – сфера S, уравнение которой может быть записано следующим образом: (x–x0)2 + (y–y0)2 + (z–z0)2 = R2, где М0(х0; y0; z0) – центр сферы, а R – её радиус. Сферу можно получить как результат вращения в пространстве окружности вокруг её диаметра.
Аналогично, при вращении эллипса вокруг одной из его осей можно получить эллипсоид вращения (рис. 1).
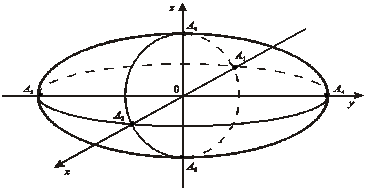
рис. 1
В грубом приближении поверхность Земли (так называемый геоид) является эллипсоидом вращения, ось вращения которого проходит через северный и южный полюсы.
Вращая гиперболу вокруг мнимой оси, получим однополостный гиперболоид вращения (рис.2)
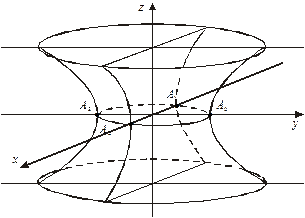
рис. 2
Если гиперболу вращать вокруг её действительной оси, то получим двуполостный гиперболоид вращения. (рис.3)
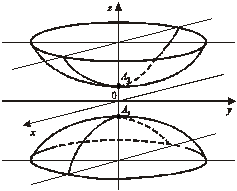
рис. 3
При вращении параболы вокруг её оси, получаем параболоид вращения (рис.4).
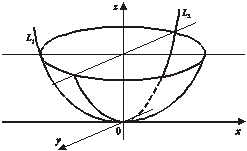
рис. 4
Отметим, что сечениями этих поверхностей плоскостями, перпендикулярными оси вращения, являются окружности.
Все выше перечисленные поверхности вращения могут быть преобразованы сжатием (растяжением) к плоскости, в которой находится ось вращения, в одноименные поверхности: эллипсоид, однополостный гиперболоид, двуполостный гиперболоид (без слова «вращения»), а параболоид вращения преобразуется в эллиптический параболоид, выпишем их уравнения:
1. 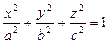 – эллипсоид;
– эллипсоид;
2. 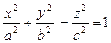 – однополостный гиперболоид;
– однополостный гиперболоид;
3. 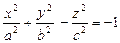 – двуполостный гиперболоид;
– двуполостный гиперболоид;
4. 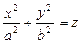 – эллиптический параболоид.
– эллиптический параболоид.
Замечания.
1. 
 Парабола обладает оптическим свойством: для светового луча, падающего из фокуса, отражённый от кривой луч лежит на прямой, параллельной оси параболы. Поэтому у параболоида вращения, или эллиптического параболоида, так же есть оптическое свойство: поместив источник света в фокус, получим, что отражённые от поверхности световые лучи окажутся параллельными оси параболоида. Это находит применение в технике (кривые зеркала в фарах, прожекторах; спутниковые антенны – тарелки в форме параболоида – принимают радио- и теле-сигналы).
Парабола обладает оптическим свойством: для светового луча, падающего из фокуса, отражённый от кривой луч лежит на прямой, параллельной оси параболы. Поэтому у параболоида вращения, или эллиптического параболоида, так же есть оптическое свойство: поместив источник света в фокус, получим, что отражённые от поверхности световые лучи окажутся параллельными оси параболоида. Это находит применение в технике (кривые зеркала в фарах, прожекторах; спутниковые антенны – тарелки в форме параболоида – принимают радио- и теле-сигналы).
2. К поверхностям второго порядка относится и гиперболический параболоид(рис. 5): 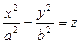 .
.
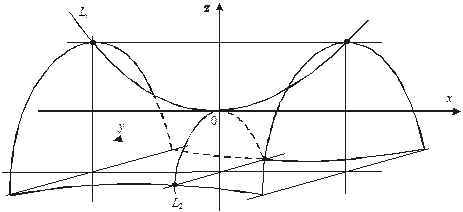
рис.5
Наряду с эллипсоидами, параболоидами и гиперболоидами рассматриваются также конические (рис.6) и цилиндрические поверхности второго порядка. Если пересечь конус плоскостями, не проходящими через его вершину, то можно получить эллипс (рис. 6), гиперболу (рис.7) и параболу (рис.8). Поэтому эти кривые называют часто коническими сечениями.
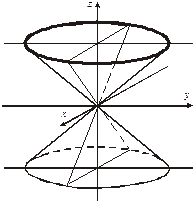
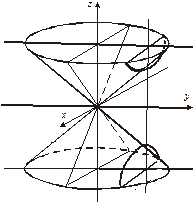
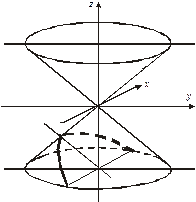
рис. 6 рис. 7 рис. 8
Уравнение конуса второго порядка с вершиной в начале системы координат OXYZ имеет вид: 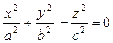 .
.
Цилиндры можно получить так: линию второго порядка переместить в пространстве в направлении, не параллельном её плоскости. Тогда из эллипса получим эллиптический цилиндр (рис.9): 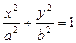 .
.
Из гиперболы получим гиперболический цилиндр (рис. 10): 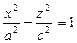 .
.
При перемещении параболы в результате имеем параболический цилиндр (рис.11): z2=2py.
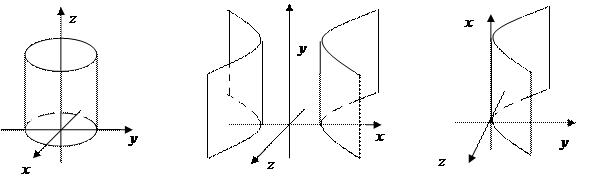
рис. 9 рис.10 рис.11
Линейная алгебра
Матрицы
Матрицей размера 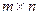 называется прямоугольная таблица из
называется прямоугольная таблица из 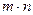 чисел, расположенных в определенном порядке в m строк и n столбцов.
чисел, расположенных в определенном порядке в m строк и n столбцов.
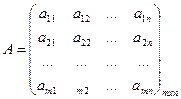
Число 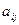 , стоящее на пересечении i-ой строки и j-го столбца, называется элементом матрицы А с номером ij. Принятое компактное обозначение для матрицы:
, стоящее на пересечении i-ой строки и j-го столбца, называется элементом матрицы А с номером ij. Принятое компактное обозначение для матрицы:
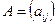
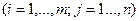
Примеры матриц:
1. 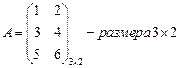 ;
;
2. 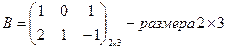
3. 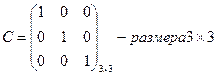
Квадратной матрицей называется матрица, у которой число строк равно числу столбцов - 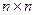 .
.
Матрицы равны между собой, если равны все соответствующие элементы этих матриц.
А=В, если 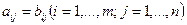
Матрица, содержащая одну строку (или столбец), называется вектором.
Например:
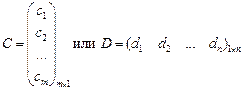
Нулевой матрицей называется матрица, у которой все элементы равны 0. 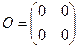
Дата добавления: 2016-06-05; просмотров: 3593;











