Собственные числа и собственные векторы линейного оператора

Собственным вектором линейного оператора j называется ненулевой вектор 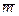, если существует действительное число l, такое, что 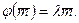Число l называется собственным числом оператора j, этому числу соответствует собственный вектор 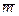. Например, при осевой симметрии плоскости относительно прямой l собственными будут: 1) все векторы, параллельные прямой l; 2) все векторы, перпендикулярные прямой l, причем, l₁=1, а l₂=–1 – собственные числа.

Рассмотрим нахождение собственных чисел и соответствующих им собственных векторов данного линейного оператора. Пусть 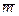– собственный вектор, соответствующий собственному числу l оператора j, заданного матрицей 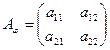в векторном пространстве V², базис которого 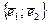. Тогда 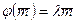; пусть .

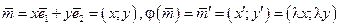Но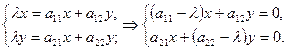

Ненулевые решения этой однородной системы существуют, если

.

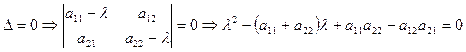Это уравнение (относительно l) называется характеристическим. Его корни – собственные числа. Найдя l_i и подставив их в однородную систему, вычислим координаты собственных векторов, соответствующих собственным числам l_i. Аналогично можно работать и в пространстве V³, V⁴ и т.д.

Замечание: если собственный вектор 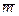- соответствует собственному числу l, то любой вектор a× 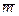– тоже собственный и соответствует этому же собственному числу l, действительно: 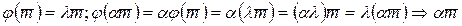– собственный вектор, соответствующий числу l.

Пример:

Пусть линейный оператор j задан своей матрицей 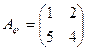. Найти его собственные числа и собственные векторы.

1. Вычислим корни характеристического уравнения 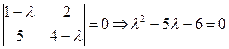. l₁=–1, l₂=6.

2. Найдём собственные векторы, соответствующие l₁=–1.

Для этого числа однородная система (на соответствующий собственный вектор), имеет вид: 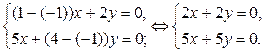Þ{x+y=0, т.е. 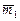=(х; –х) – их бесчисленное множество (т.к. х – любое, кроме 0). В частности, если х=1, то 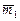=(1; –1).

Далее так же находим собственный вектор и для l₂=6.

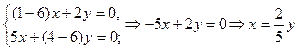, т.е. 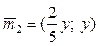, здесь Y¹0. В частности, если у=5, то 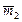=(2; 5).