Прямая в пространстве

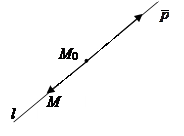
Для задания и вывода уравнений рассмотрим точку М₀(х₀; y₀; z₀) в координатном пространстве OXYZ и ненулевой вектор 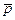=(a; b; g). Тогда в пространстве найдётся только одна прямая l , проходящая через точку М₀ в направлении вектора 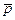. М₀ и 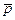называются начальной точкой и направляющим вектором прямой l соответственно.

Для любой точки МÎl имеем, что

.

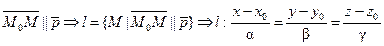Получили канонические уравнения прямой l.

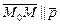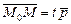Û , где t Îℝ Þ x–x₀ =at, y–y₀ =bt, z–z₀ =gt, или

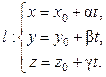– параметрические уравнения прямой l.

Прямую в пространстве можно задать парой пересекающихся плоскостей, а именно:
l =w₁ Ç w₂ Þ l: 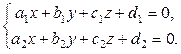– общие уравнения прямой l.

Угол между прямой и плоскостью

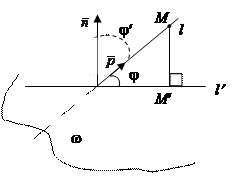
Пусть j= 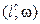, тогда j = 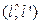, где l′ – проекция прямой 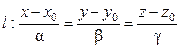на плоскость w: aх+bу+cz+d=0.

Очевидно, что 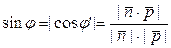, где j¢= .

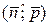Вопросы для самопроверки

1. Чем задаётся плоскость в пространстве?

2. Каков геометрический смысл старших коэффициентов в уравнении плоскости.

3. Вывести уравнения координатных плоскостей XOY, XOZ, YOZ.

4. Установить, параллельны ли плоскости 2x+3y–z+1=0 и 4x+6y–2z–5=0.

5. Проверить перпендикулярность плоскостей 3x–2y+z+1=0 и x+y–z–5=0.

6. Вычислить расстояние от точки М₀(3; 2; 1) до плоскости w: x+y–z+5=0.

7. Выписать начальную точку и направляющий вектор прямой .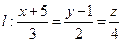

8. Выписать канонические и параметрические уравнения координатных осей OX, OY, OZ в пространстве.

9. Написать общие уравнения координатных осей в пространстве.

10. Вычислить угол между прямой 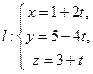и плоскостью w: 2x+3y–z+1=0.