Приведение матрицы линейного оператора к диагональному виду

Ранее было отмечено, что вид матрицы А_j линейного оператора j зависит от того, в каком базисе её рассмотреть. Если за базис принять базис из собственных векторов этого оператора, то матрица А¢_j будет иметь диагональный вид, причём на диагонали этой матрицы будут стоять собственные числа. Напомним A¢_j=T^-1 ×A_j×Т. Покажем это на примере.

Пусть 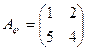. Для этого оператора были найдены l₁=–1, l₂=6 и собственные векторы 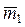=(1; –1) и 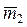=(2; 5) соответственно. Рассмотрим новый базис { 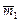; 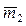}, тогда матрица перехода получит вид .

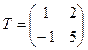1. Т^–1 –? .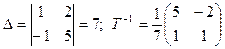

Проверка: Т^–1Т = .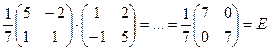

2. Т^–1×A_j= .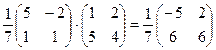

3. T^-1 ×A_j×Т= .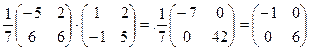

Итак, A¢_j=T^-1 ×A_j×Т= 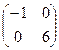– диагональная матрица (на диагонали – собственные числа).

Квадратичные формы

Однородный многочлен второй степени относительно переменных х, у (т.е. каждый его одночлен – второй степени) называется квадратичной формой от этих переменных:
Ф(x, y)=a₁₁x²+2a₁₂xy+a₂₂y². Квадратичная форма Ф вполне определяется матрицей вида: 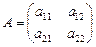, где а₂₁=а₁₂, т.е. это – симметричная матрица.

Если перейти к новому базису, то квадратичная форма, как и её матрица, изменит свой вид, но останется квадратичной относительно новых переменных x ¢, y ¢. Как уже отмечалось, в базисе из собственных векторов матрица линейного оператора имеет диагональный вид, поэтому, квалифицируя матрицу квадратичной формы как матрицу некоторого линейного оператора, приведём её к диагональному виду выше рассмотренным способом.

Например, пусть имеем квадратичную форму:

Ф (x, y) = 17x2 + 12xy + 8y2.

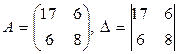= 136 – 36 = 100 > 0.

Для оператора с этой матрицей собственными числами являются l₁=5, l₂=20. Тогда в базисе из собственных векторов, соответствующих этим числам, матрица этого оператора, а значит, и матрица этой квадратичной формы, примет вид: 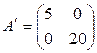, и соответственная квадратичная форма запишется так: Ф(x¢; y¢)=5(x¢)²+20(y¢)².