Матричные модели в биологии

Пример 1. Контакты первого и второго порядка в эпидемиологии.

Предположим, имеется группа из 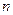больных некоторой заразной болезнью, будем считать ее первой группой. Ко второй группе отнесем 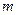людей, опрашиваемых на предмет выявления контактов с людьми из первой группы. Кроме того, можно составить третью группу из 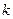человек, опрашиваемых для выяснения контактов с людьми из второй группы.

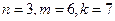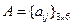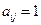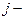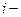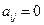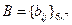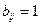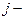В частности, принимая , определим матрицу контактов между второй и первой группами , полагая если й человек из второй группы находился в контакте с м больным из первой группы и – в противном случае. Аналогично определим матрицу контактов между третьей и второй группами , полагая если й человек из третьей группы находился в контакте с 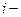м больным из второй группы и 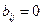- в противном случае.

Матрицы 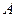и 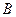описывают схемы прямых контактов между группами. Предположим

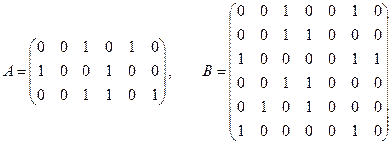(1)

Нас могут интересовать непрямые контакты или контакты второго порядка между людьми из третей группы (7 человек) и больными из первой группы (3 человека). Матрица 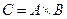будет описывать эти непрямые контакты, в данном случае:

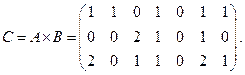(2)

Например элемент 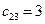(матрицы 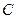) показывает, что имеется 2 непрямых контакта между третьим человеком из третьей группы и вторым человеком из первой группы. По виду матрицы 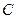можно сделать некоторые предварительные выводы о вероятности заражения лиц третьей группы в результате непрямых контактов с больными. Суммируя элементы шестого столбца, определяем что у 6 человека из третьей группы оказалось 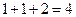непрямых контакта с группой больных, что может свидетельствовать о высокой вероятности его заражения. В то время как у 5 человека непрямые контакты отсутствуют и его, видимо, можно исключить из группы "возможных контактов".

Пример 2. Матричная модель популяции.

В любой популяции, будь то популяция рыб, лосей, крупного рогатого скота и т.д, можно условно выделить несколько возрастных групп. В простейшем случае можно рассматривать 3 группы: препродуктивную (еще не способны к воспроизведению потомства), обозначим 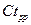, репродуктивную 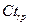- производящую потомство и постпродуктивную 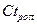- не производящую потомство по старости.

В зависимости от конкретной задачи может быть рассмотрена более детальная возрастная градация, например, градация возраста по годам, но мы ограничимся упомянутыми простейшими случаями. Будем отслеживать численность возрастных групп популяции в моменты времени 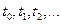Обозначим 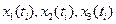- численности, соответственно, препродуктивной, репродуктивной и постпродуктивной групп в момент 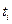. Интервал времени 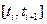можно выбрать таким образом, чтобы за этот период особи предыдущей возрастной группы перешли в последующую. В начальный момент состояние популяции опишется вектор-столбцом:

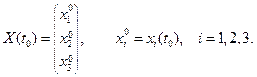(3)

В последующий момент 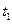можно принять 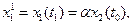то есть численность новорожденных пропорциональна численности репродуктивных особей в предыдущий момент ( 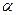- коэффициент "рождаемости"). Далее примем 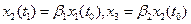( 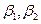- коэффициенты "выживаемости", соответственно первой и второй возрастных групп). Будем считать коэффициенты 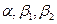константами, одинаковыми для всех моментов времени. По смыслу задачи эти коэффициенты положительны, причем 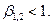Состояние популяции в момент 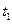выражается:

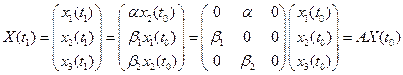(4)

Аналогично:

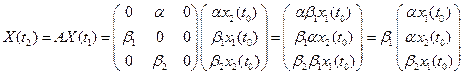(5)

Продолжая выражать состояние популяции в последующий момент через предыдущий, имеем

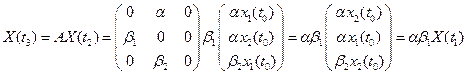(6)

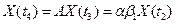(7)

Общую формулу для 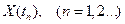можно представить в виде:

а) Если 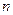- четно, то 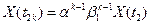(8)

б) Если 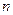- нечетно, то 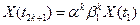(9)

В соответствии с формулами, можно сделать некоторые выводы:

1) Численность популяции растет при 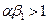. Действительно, в этом случае 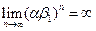, а значит все компоненты вектора 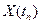возрастают как при четном, так и при нечетном 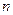. Исходя из того, что коэффициенты 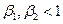, неравенство 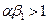будет выполнятся при достаточно большом коэффициенте "выживаемости" .

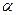Если 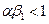,то 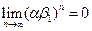и все компоненты вектора 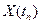стремятся к нулю. Популяция погибает.

В случае 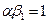, 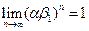очевидно, численность популяции со временем не возрастает и не уменьшается. В четные моменты времени она равна 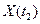, а в нечетные 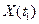, своего рода колебательный процесс. В частности такая картина будет наблюдаться, если 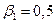(половина "препродуктивной" группы не доживает до зрелого возраста), а 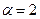(выжившие взрослые особи увеличивают численность в двое).

2)Существенность различия численности популяции в четные и нечетные моменты времени. Продемонстрируем это она примере популяции, у которой в начальный момент имеюются особи только препродуктивной группы (для популяции рыб - выпускание мальков в необитаемый водоем).

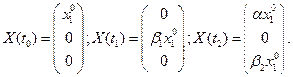(10)

Согласно формулам

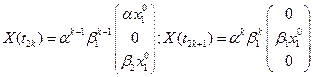(11)

то есть в четные моменты времени отсутствуют особи репродуктивной группы, а в нечетные - препродуктивной и постпродуктивной групп.

3)Отношение численностей различных возрастных групп со временем сохраняет определенное постоянство. Так из (8) следует:

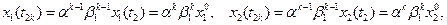
откуда:

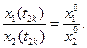
Аналогично:

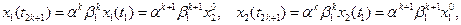
откуда:

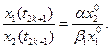
Аналогично показывается постоянство соотношений численностей первой и третьей или второй и третьей возрастных групп.