Правило Крамера для 3-мерного случая
Если для системы (7) 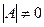 , то она имеет единственное решение, которое находится по формулам:
, то она имеет единственное решение, которое находится по формулам:
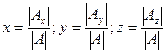 ;
;
В случае, если 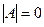 , то система либо имеет бесконечное множество решений ( когда
, то система либо имеет бесконечное множество решений ( когда 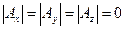 ), либо не имеет решений или несовместна ( в противном случае).
), либо не имеет решений или несовместна ( в противном случае).
Пример.Решить систему линейных уравнений:
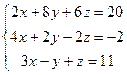
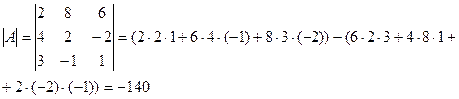
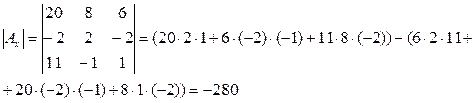
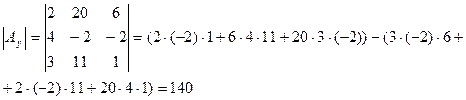

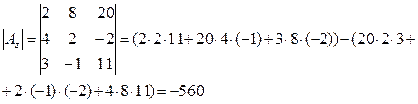
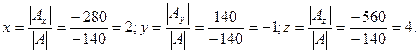
Обратная матрица
Как уже было отмечено, АВ ≠ ВА, но имеются и для этого закона исключения:
АЕ = ЕА, где А, Е – квадратные матрицы, причем Е – единичная матрица.
А*А=АА*, где А* – матрица, присоединенная к матрице А.
Присоединенная матрица А*= 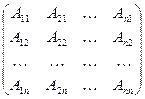 состоит из элементов Аij – алгебраических дополнений к элементам аij данной матрицы А. Алгебраическое дополнение к элементу аij есть тот определитель, который получен из определителя матрицы А «вычёркиванием» строки и столбца элемента аij , причём этот (полученный) определитель берётся со знаком плюс, если сумма (i+j) – чётная, и со знаком минус, если – нечётная.
состоит из элементов Аij – алгебраических дополнений к элементам аij данной матрицы А. Алгебраическое дополнение к элементу аij есть тот определитель, который получен из определителя матрицы А «вычёркиванием» строки и столбца элемента аij , причём этот (полученный) определитель берётся со знаком плюс, если сумма (i+j) – чётная, и со знаком минус, если – нечётная.
Пример. Пусть А = 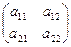 , тогда а11 → А11=а22, а12 → А12= –а21, а21 → А21= –а12 , а22 → А22 = а11. А*=
, тогда а11 → А11=а22, а12 → А12= –а21, а21 → А21= –а12 , а22 → А22 = а11. А*= 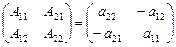
Нетрудно проверить, что А*А=АА*= |A| E = |A| 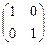 .
.
Невырожденные матрицы – квадратные матрицы с отличным от нуля определителем. Для таких матриц существуют обратные, а именно: матрица А-1 называется обратной к матрице А, если А-1А=АА-1=Е.
Учитывая А∙А*=А*∙А= 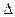 ∙Е, получим, что А-1=
∙Е, получим, что А-1= 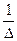 А*. Это один из способов нахождения обратной матрицы.
А*. Это один из способов нахождения обратной матрицы.
Пример: Найти матрицу, обратную к матрице 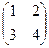 .
.
Решение. 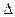 =
= 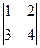 =–2, А11=4, А21=–2, А12=–3, А22=1.
=–2, А11=4, А21=–2, А12=–3, А22=1.
А-1= 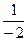
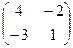 =
= 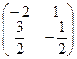 . Проверку сделать самостоятельно.
. Проверку сделать самостоятельно.
Замечание. Для произведения матриц выполняется ассоциативный закон: (AB)С=A(BC).
Пример. Проверить равенство
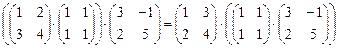 .
.
Дата добавления: 2016-06-05; просмотров: 1439;











