Интегральные уравнения типа «свертки».
Интегральным уравнением называется уравнение, содержащее искомую функцию под знаком интеграла.
Например, 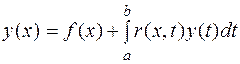 (8.10)
(8.10)
-это линейное интегральное уравнение Фредгольма второго рода.
Здесь y(x) – неизвестная функция,
f(x) и r(x,t) – заданные функции.
Функцию r(x,t) называют ядром уравнения (8.10),
a и b=const.
Изменим (8.10) следующим образом.
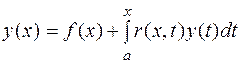 (8.11)
(8.11)
Получим линейное интегральное уравнение Вольтерра 2го рода.
Если в (8.10) и (8.11) 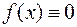 , то уравнения будут называться однородными.
, то уравнения будут называться однородными.
Если искомая функция y(x) входит только под знак интеграла, то (8.10) и (8.11) преобразуются в уравнения Фредгольма и Вольтерра 1го рода.
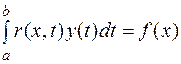 или
или 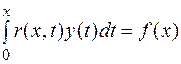 .
.
Совершенно очевидно, что большую роль в решении будет играть ядро уравнения, т.е. функция r(x,t). Важный класс уравнений Вольтерра получается, если ядро r(x,t) зависит только от разности
r(x,t)=r(x-t).
Уравнение в этом случае имеет вид.
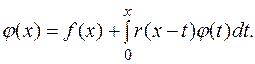 (8.12)
(8.12)
Его еще называют уравнением типа свертки.
Пусть входящие в уравнение (8.12) функции удовлетворяют условиям оригинала, тогда может быть найдено изображение функций по Лапласу
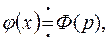
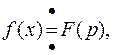
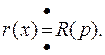
Пользуясь формулой свертки, получим операторное уравнение
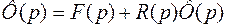 .
.
Откуда
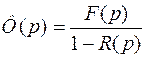 .
.
Для Ф(р) находим 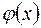 - решение интегрального уравнения (8.12).
- решение интегрального уравнения (8.12).
Пример. Решить интегральное уравнение
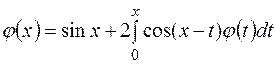 .
.
Решение:
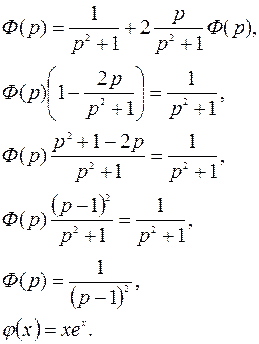
Так же решаются и системы интегральных уравнений.
Пример. Решить систему интегральных уравнений
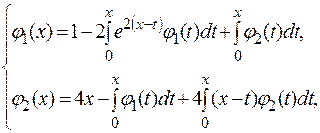 в области изображений получим:
в области изображений получим:
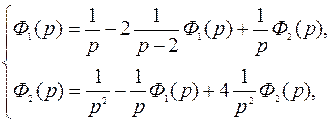 преобразовав, будем иметь:
преобразовав, будем иметь:
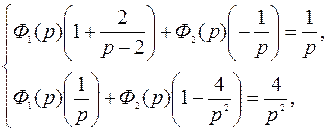 или,
или,
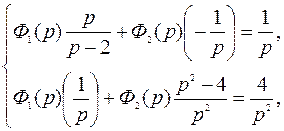 решим методом Крамера:
решим методом Крамера:
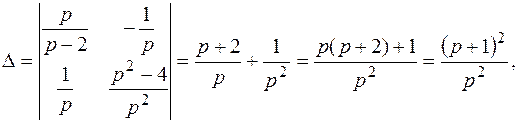
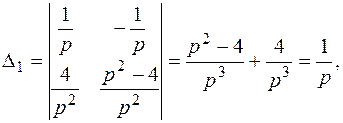
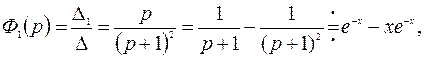
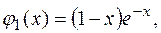
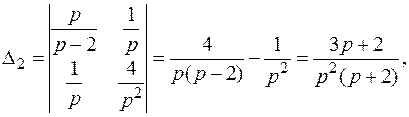
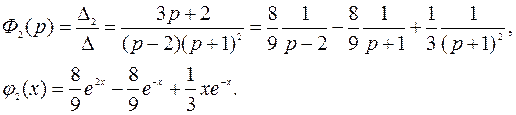
Дата добавления: 2021-11-16; просмотров: 443;











