Решение дифференциальных уравнений с постоянными коэффициентами с помощью интеграла Дюамеля.

.

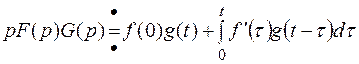Пусть требуется решить линейное дифференциальное уравнение с постоянными коэффициентами n-го порядка.

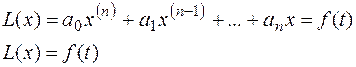(8.2)

при нулевых начальных условиях.

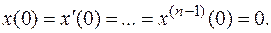(8.3)

Пусть нам известно решение уравнения

L(x) = 1, (8.4)

при тех же начальных условиях (8.3).

Это решение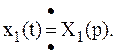

Операторное уравнение (8.4) будет иметь вид:

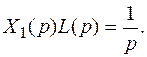(8.5)

Откуда,

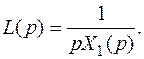(8.6)

Операторное уравнение (8.2).

X(p)L(p)=F(p). (8.7)

Откуда

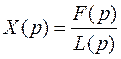
или с учетом (8.6)

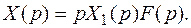(8.8)

Теперь в силу интеграла Дюамеля, получим

.

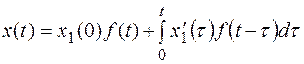А так как начальные условия нулевые

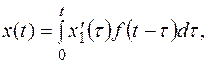
где 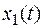- решение уравнения с единичной правой частью. Т.о. зная решение для единичной правой части, при помощи интегрирования найдем решение для любой правой части.

Пример. Найти частное решение уравнения

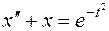
при нулевых начальных условиях.

Решение: Здесь правая часть не является оригиналом 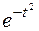, не удовлетворяет третьему условию оригинала.

Рассмотрим уравнение:

.

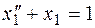Операторное уравнение имеет вид:

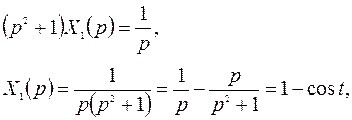
таким образом 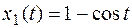- это решение уравнения при единичной правой части.

Тогда .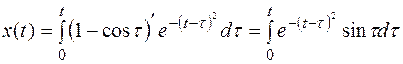

Выразить полученный интеграл с помощью элементарных функций не удается и обычно ищется приближенное решение.