Графическое изображение вариационных рядов.

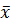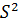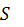Для визуального подбора теоретического распределения, а также выявления положения среднего значения ( ) и характера рассеивания ( и ) вариационные ряды изображают графически.

Полигон и кумулята применяются для изображения как дискретных, так и интервальных рядов, гистограмма – для изображения только интервальных рядов. Для построения этих графиков запишем вариационные ряды распределения (интервальный и дискретный) относительных частот (частостей) 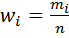, накопленных относительных частот 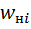и найдём отношение 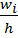, заполнив таблицу 4.

Таблица 4

Статистический ряд распределения линейных размеров

диаметров 100 втулок

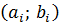
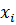
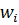
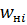
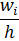
4,97 – 5,08	5,03	0,02	0,02	0,18
5,08 – 5,19	5,14	0,03	0,05	0,27
5,19 – 5,30	5,25	0,12	0,17	1,09
5,30 – 5,41	5,36	0,19	0,36	1,73
5,41 – 5,52	5,47	0,29	0,65	2,64
5,52 – 5,63	5,58	0,18	0,83	1,64
5,63 – 5,74	5,69	0,13	0,96	1,18
5,74 – 5,85	5,80	0,04		0,36
	-	1,00	-	-

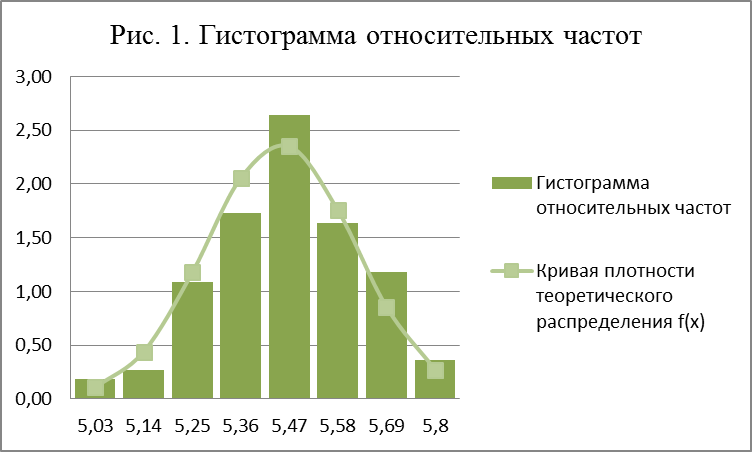
Для построения гистограммы относительных частот (частостей) на оси абсцисс откладываем частичные интервалы, на каждом из которых строим прямоугольник, площадь которого равна относительной частоте 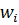данного i-го интервала. Тогда высота элементарного прямоугольника должна быть равна 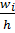, где в нашем примере h=0,11 мм (рис. 1). Следовательно, площадь под гистограммой равна сумме всех относительных частот, т.е. единице.

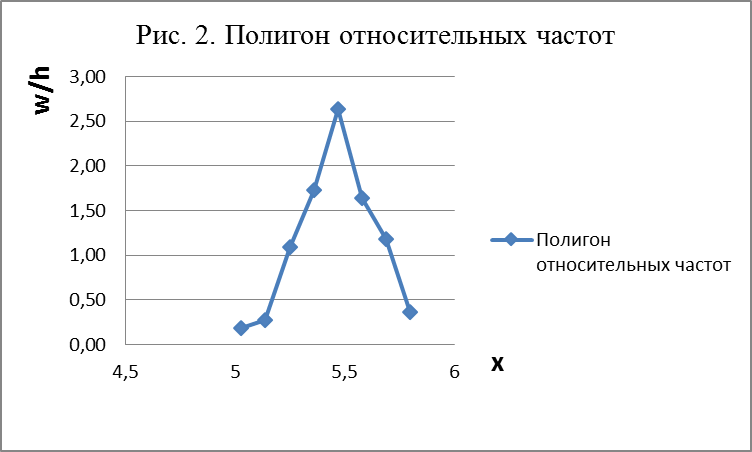
Из гистограммы можно получить полигон того же распределения, если середины верхних оснований прямоугольников соединить отрезками прямых (рис. 2).

Гистограмма и полигон являются аппроксимациями кривой плотности (дифференциальной функции) теоретического распределения (генеральной совокупности). Поэтому по их виду можно судить о гипотетическом законе распределения.

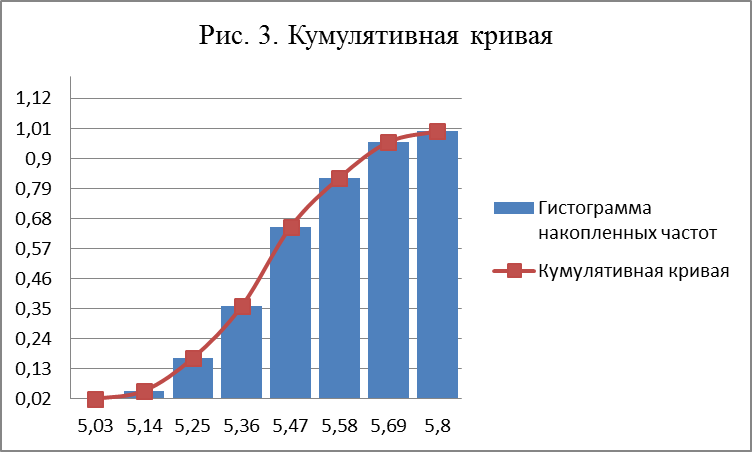
Для построения кумуляты дискретного ряда по оси абсцисс откладывают значения признака 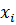, а по оси ординат – накопленные относительные частоты 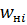. Для интервального ряда по оси абсцисс откладывают интервалы (рис. 3).

С кумулятой сопоставляется график интегральной функции распределения F(x).

В нашем примере коэффициенты асимметрии и эксцесса не намного отличаются от нуля. Коэффициент асимметрии оказался отрицательным ( 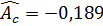), что свидетельствует о небольшой левосторонней асимметрии данного распределения. Эксцесс оказался также отрицательным ( 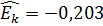). Это говорит о том, что кривая, изображающая ряд распределения, по сравнению с нормальной, имеет несколько более плоскую вершину. Гистограмма и полигон напоминают кривую нормального распределения (рис. 1 и рис. 2). Всё это даёт возможность выдвинуть гипотезу о том, что распределение линейных размеров диаметра втулок является нормальным.